Advertisements
Advertisements
Question
A cell of e.m.f. 1.8V and internal resistance 2Ω is connected in series with an ammeter of resistance 0.7Ω and a resistor of 4.5Ω as shown in Fig.
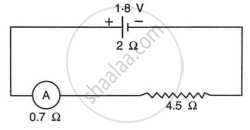
- What would be the reading of the ammeter?
- What is the potential difference across the terminals of the cell?
Solution
The resistances are series connected
∴ Total resistance of circuit = (r + R)
(r + R) = (2 + 0.7 + 4.5)
= 7.2 Ω
e.m.f. of cell = 1.8 V
- Reading of Ammeter `I = "V"/("R" + r)`
= `("e.m.f")/("R" + r)`
`I = 1.8/7.2`
= 0.25 A - Potential difference across the terminals of the cell = IR
`"V" = 1/4 xx 5.2`
V = 1.3 V
R = 4.5 + 0.7
R = 5.2 Ω
APPEARS IN
RELATED QUESTIONS
Name two factors on which the internal resistance of a cell depends and state how does it depend on the factors stated by you.
A cell of e.m.f ε and internal resistance r is used to send current to an external resistance R. Write expressions for
- the total resistance of circuit.
- the current drawn from the cell.
- the p.d. across the cell.
- voltage drop inside the cell.
A cell is used to send current to an external circuit.
- How does the voltage across its terminals compare with its e.m.f.?
- Under what condition is the e.m.f. of a cell equal to its terminal voltage?
A battery of e.m.f. 15 V and internal resistance 3 ohm is connected to two resistors of resistances 3 ohm and 6 ohm is series Find:
(a) the current through the battery
(b) the p.d. between the terminals of the battery.
A cell of e.m.f. ε and internal resistance 𝔯 sends current 1.0 A when it is connected to an external resistance 1.9 Ω. But it sends current 0.5 A when it is connected to an external resistance 3.9 Ω. Calculate the values of ε and 𝔯.
A cell of emf. 1.5 V and internal resistance 10 ohms is connected to a resistor of 5 ohms, with an ammeter in series see fig.. What is the reading of the ammeter?
Define the e.m.f. (E) of a cell and the potential difference (V) of a resistor R in terms of the work done in moving a unit charge. State the relation between these two works and the work done in moving a unit charge through a cell connected across the resistor. Take the internal resistance of the cell as ‘r’. Hence obtain an expression for the current i in the circuit.
Four cells each of e.m.f. 2V and internal resistance 0.1 Ω are connected in series to an ammeter of negligible resistance, a 1.6 Ω resistor and an unknown resistor R1. The current in the circuit is 2A. Draw a labelled diagram and calculate:
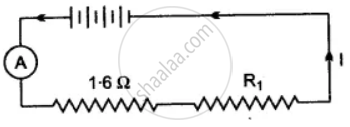
(i) Total resistance of the circuit,
(ii) Total e.m.f.
(iii) The value of R1 and
(iv) The p.d. across R1.
When a resistance of 3Ω is connected across a cell, the current flowing is 0.5 A. On changing the resistance to 7Ω, the current becomes 0.25A. Calculate the e.m.f. and the internal resistance of the cell.
A battery of e.m.f. 6·0 V supplies current through a circuit in which the resistance can be changed. A high resistance voltmeter is connected across the battery. When the current is 3 A, the voltmeter reads 5.4 V. Find the internal resistance of the battery.
