Advertisements
Advertisements
Question
A cell of emf. 1.5 V and internal resistance 10 ohms is connected to a resistor of 5 ohms, with an ammeter in series see fig.. What is the reading of the ammeter?
Solution

E = i (R + r)
1.5 = i(5 + 10)
⇒ `1.5/15`
i = 0.1 Å.
APPEARS IN
RELATED QUESTIONS
What happens to the resistivity of semiconductor with the increase of temperature?
A cell of Emf 2 V and internal resistance 1.2 Ω is connected with an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in the diagram below:
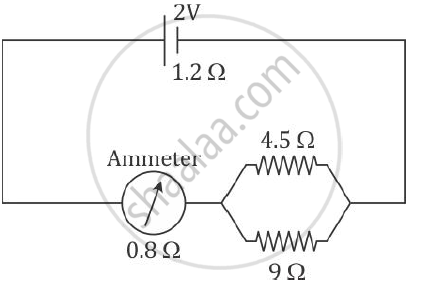
1) What would be the reading on the Ammeter?
2) What is the potential difference across the terminals of the cell?
A cell of e.m.f. 1.8V and internal resistance 2Ω is connected in series with an ammeter of resistance 0.7Ω and a resistor of 4.5Ω as shown in Fig.
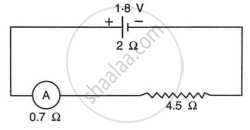
- What would be the reading of the ammeter?
- What is the potential difference across the terminals of the cell?
A battery of e.m.f. 15 V and internal resistance 3 ohm is connected to two resistors of resistances 3 ohm and 6 ohm is series Find:
(a) the current through the battery
(b) the p.d. between the terminals of the battery.
Define the e.m.f. (E) of a cell and the potential difference (V) of a resistor R in terms of the work done in moving a unit charge. State the relation between these two works and the work done in moving a unit charge through a cell connected across the resistor. Take the internal resistance of the cell as ‘r’. Hence obtain an expression for the current i in the circuit.
Four cells each of e.m.f. 2V and internal resistance 0.1 Ω are connected in series to an ammeter of negligible resistance, a 1.6 Ω resistor and an unknown resistor R1. The current in the circuit is 2A. Draw a labelled diagram and calculate:
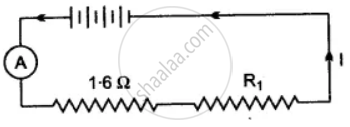
(i) Total resistance of the circuit,
(ii) Total e.m.f.
(iii) The value of R1 and
(iv) The p.d. across R1.
A cell supplies a current of 0.6 A through a 2Ω coil and a current of 0.3 A through on 8Ω coil. Calculate the e.m.f and internal resistance of the cell.
When a resistance of 3Ω is connected across a cell, the current flowing is 0.5 A. On changing the resistance to 7Ω, the current becomes 0.25A. Calculate the e.m.f. and the internal resistance of the cell.
Explain the meaning of the term internal resistance of a cell.
A battery of e.m.f. 6·0 V supplies current through a circuit in which the resistance can be changed. A high resistance voltmeter is connected across the battery. When the current is 3 A, the voltmeter reads 5.4 V. Find the internal resistance of the battery.
