Question

A circle touches two of the smaller sides of a ΔABC (a < b < c) and has its centre on the greatest side. Then the radius of the circle is ______.

Options

• `(a - b - c)/2`

• `(abc)/2`

• `(2Δ)/(a + b)`

• `(a + b + c)/2`

Answer 1

A circle touches two of the smaller sides of a ΔABC (a < b < c) and has its centre on the greatest side. Then the radius of the circle is `underlinebb((2Δ)/(a + b))`.

Explanation:

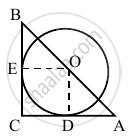
Let OD = OE = r 

In ΔODA

`(OD)/(OA)` = sinA

⇒ OA = `r/sinA`  ...(1)

In ΔOEB

`(OE)/(OB)` = sinB

⇒ OB = `r/sinB`  ...(2)

Adding (1) and (2)

OA + OB = c = `r/sinA + r/sinB`

⇒ `r((bc)/(2Δ) + (ac)/(2Δ))` = c  ...[∵ Δ = `1/2`bc sin A]

⇒ r = `(2Δ)/(b + a)`