Advertisements
Advertisements
Question
A convex lens is of focal length 20 cm. Find its power.
Solution
Given: Focal length f = 20cm = 0.2 m
Power = `1/"Focal length in m"=1/0.2` = 5D
APPEARS IN
RELATED QUESTIONS
Define the power of a lens.
The lens mentioned in 6(b) above is of focal length 25cm. Calculate the power of the lens.
The power of a lens is +2.0D. Its focal length should be :
On reducing the focal length of a lens, its power ______.
Consider three converging lenses L1, L2 and L3 having identical geometrical construction. The index of refraction of L1 and L2 are \[\mu_1 \text{ and } \mu_2\] respectively. The upper half of the lens L3 has a refractive index \[\mu_1\] and the lower half has \[\mu_2\] following figure . A point object O is imaged at O1 by the lens L1 and at O2 by the lens L2placed in same position. If L3 is placed at the same place,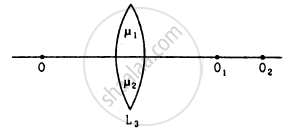
(a) there will be an image at O1
(b) there will be an image at O2.
(c) the only image will form somewhere between O1 and O2
(d) the only image will form away from O2.
A double convex lens has focal length 25 cm. The radius of curvature of one of the surfaces is double of the other. Find the radii, if the refractive index of the material of the lens is 1.5.
A 5.0 diopter lens forms a virtual image which is 4 times the object placed perpendicularly on the principal axis of the lens. Find the distance of the object from the lens.
If there is a convex lens of focal length 75 cm and a concave lens of focal length 40 cm, then calculate their combined power and combined focal length.
A convex lens with radii of curvature R1 = R2 is immersed in water. Assuming that the refractive indices of glass and water are 3/2 and 4/3 respectively, its focal length f1 in comparison to that in air, f, is ______.
An object is placed in front of a converging lens. Obtain the conditions under which the magnification produced by the lens is
- negative and
- positive.
