Question

A convex lens made up of glass of refractive index 1.5 is dipped, in turn, in (i) a medium of refractive index 1.6, (ii) a medium of refractive index 1.3.

(a) Will it behave as a converging or a diverging lens in the two cases?

(b) How will its focal length change in the two media?

Answer 1

Given Refractive index of glass, μ_a = 1.5

Refractive index of I^st medium, μ₁ = 1.6

Refractive index of II^nd medium, μ₂ = 1.3

(a) For I^st medium

`mu_1 > mu_a => mu_a/mu_1<1`

Hence, f > 0; concave lens or diverging lens

(ii) For II^nd medium

`mu_2 > mu_a => mu_a/mu_2<1`

Hence, f < 0; convex lens or converging lens

(b)

(i) For first medium,

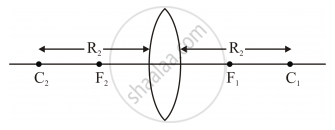
`1/f_1  = (1-(mu_a)/(mu_1))(1/R_1  - 1/R_2)_(-R_2 >0)^(R_1>0)`

`=(1 - 1.5/1.6)`         (Positive number) for convex lens

`(1-0.9)`                    (Positive number)  

`=(0.1)`                    (Positive number) 

Original focal length

`1/f =(1-mu_0)(1/R_1  - 1/R_2)`

`1/f = -0.5`  (Positive number) 

`=> f_1/f  = -0.5/0.1`

`=> f_1 = -5f`

Hence, focal length will be 5 times the original focal length and its nature will become diverging.

(ii) For second medium

`1/f_2  = (1-(mu_0)/mu_2) (1/R_1 - 1/R_2)`

`=(1 - 1.5/1.3) (1/R_1 - 1/R_2)`

`(1 -1.15)(1/R_1 - 1/R_2)`

`= 0.2 (1/R_1 -1/R_2)`

`=> f_2 /f = (0.2)/(0.1)`

`=> f_2 =2f`

Hence, focal length will be twice the original focal length and its nature (Converging nature) will remain same.