Advertisements
Advertisements
Question
A curved surface is shown in figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.

With the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.
- For which balls is total mechanical energy conserved?
- Which ball (s) can reach D?
- For balls which do not reach D, which of the balls can reach back A?
Solution
- A ball 1 is rolling down without slipping there is no dissipation of energy hence, total mechanical energy is conserved. Bail 3 is having negligible friction hence, there is no loss of energy.
- Ball 1 acquires rotational energy, ball 2 loses energy by friction. They cannot cross at C. Ball 3 can cross over.
- Ball 1 and 2 turn back before reaching C. Because of loss of energy, ball 2 cannot reach back to A. Ball 1 has a rotational motion in the “wrong” sense when it reaches B. It cannot roll back to A, because of kinetic friction.
APPEARS IN
RELATED QUESTIONS
A body of mass 0.5 kg travels in a straight line with velocity v = `ax^(3/2)` where a = `5 m^(1/2)` s-1. What is the work done by the net force during its displacement from x = 0 to x = 2 m?
The two ends of a spring are displaced along the length of the spring. All displacement have equal magnitudes. In which case or cases the tension or compression in the spring will have a maximum magnitude ?
(a) the right end is displaced towards right and the left end towards left
(b) both ends are displaced towards right
(c) both ends are displaced towards left
(d) the right end is displaced towards left and the left end towards right.
Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
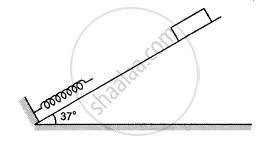
Following figure shows a spring fixed at the bottom end of an incline of inclination 37°. A small block of mass 2 kg starts slipping down the incline from a point 4⋅8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find (a) the friction coefficient between the plane and the block and (b) the spring constant of the spring. Take g = 10 m/s2.
A block of mass m moving at a speed ν compresses a spring through a distance x before its speed is halved. Find the spring constant of the spring.
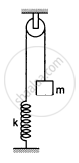
Consider the situation shown in the following figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the pulley, find the maximum elongation of the spring.
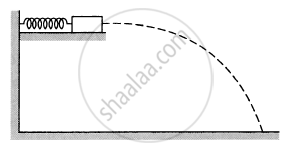
A small block of mass 100 g is pressed against a horizontal spring fixed at one end to compress the spring through 5 cm (figure following). The spring constant is 100 N/m. When released, the block moves horizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
If a spring extends by x on loading, then energy stored by the spring is (T is the tension in the spring and k is the spring constant)
A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero.
An engine is attached to a wagon through a shock absorber of length 1.5 m. The system with a total mass of 50,000 kg is moving with a speed of 36 km h–1 when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of energy of the wagon is lost due to friction, calculate the spring constant.
