Advertisements
Advertisements
Question
A diverging lens of focal length 20 cm and a converging lens of focal length 30 cm are placed 15 cm apart with their principal axes coinciding. Where should an object be placed on the principal axis so that its image is formed at infinity?
Solution
Given,
Focal length of convex lens, fc = 30 cm
Focal length of concave lens, fd = 15 cm
Distance between both the lenses, d = 15 cm
Let (f) be the equivalent focal length of both the lenses.\[\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2} - \frac{d}{f_1 f_2}\]
\[ = \frac{1}{30} + \left( \frac{1}{20} \right) - \left( \frac{5}{30( - 20)} \right)\]
\[ = \frac{1}{120}\]
\[\Rightarrow f=120 \text{ cm }\]
As focal length is positive, so it will be a converging lens.
Let 'd1' be the distance from diverging lens, so that the emergent beam is parallel to the principal axis and the image will be formed at infinity.
\[d_1 = \frac{df}{f_c} = \frac{15 \times 120}{30} = 60 \text{ cm }\]
It should be placed 60 cm left to the diverging lens. The object should be placed
(120 − 60) = 60 cm from the diverging lens
Let d2 be the distance from the converging lens. Then,
\[d_2 = \frac{df}{f_d} = \frac{15 \times 120}{20}\]
d2 = 90 cm
Thus, it should be placed (120 + 90) cm = 210 cm right to converging lens.
APPEARS IN
RELATED QUESTIONS
Which of the two has a greater power: a lens of short focal length or a lens of large focal length?
What is the nature of a lens whose power is, −4 D?
What is the unit of power of a lens? Define the unit of power of a lens.
On reducing the focal length of a lens, its power ______.
A symmetric double convex lens in cut in two equal parts by a plane perpendicular to the principal axis. If the power of the original lens was 4 D, the power a cut-lens will be
A pin of length 2.00 cm is placed perpendicular to the principal axis of a converging lens. An inverted image of size 1.00 cm is formed at a distance of 40.0 cm from the pin. Find the focal length of the lens and its distance from the pin.
Consider the situation described in the previous problem. Where should a point source be placed on the principal axis so that the two images form at the same place?
Which lens has more power a thick lens or a thin lens?
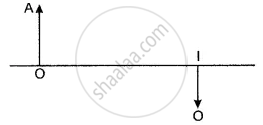
The following diagram shows the object O and the image I formed by a lens. Copy the diagram and on it mark the positions of the lens LL’ and focus (F). Name the lens.
Complete the diagram to show the formation of the image of the object AB.
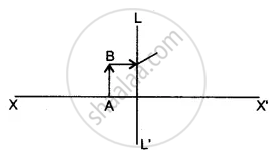
(i) Name the Lens LL’.
(ii) Where is the image of the object AB formed?
(iii) State three characteristics of the image.
The power of the magnifying glass depends on the distance of the magnifying glass from object.
Find the power of a convex lens of focal length of + 25 cm.
Power of a lens is – 4D, then its focal length is
According to Rayleigh’s scattering law, the amount of scattering of light is inversely proportional to the fourth power of its ______.
Match the following:
| Column - I | Column - II | ||
| 1 | Retina | a | Path way of light |
| 2 | Pupil | b | Far point comes closer |
| 3 | Ciliary muscles | c | near point moves away |
| 4 | Myopia | d | Screen of the eye |
| 5 | Hypermetropia | e | Power of accommodation |

The above lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.
A convex lens with radii of curvature R1 = R2 is immersed in water. Assuming that the refractive indices of glass and water are 3/2 and 4/3 respectively, its focal length f1 in comparison to that in air, f, is ______.
