Advertisements
Advertisements
Question
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
Solution
Let the factory manufacture x screws of type A and y screws of type B on each day. Therefore,
x ≥ 0 and y ≥ 0
The given information can be compiled in a table as follows.
| Screw A | Screw B | Availability | |
| Automatic Machine (min) | 4 | 6 | 4 × 60 =240 |
| Hand Operated Machine (min) | 6 | 3 | 4 × 60 =240 |
The profit on a package of screws A is Rs 7 and on the package of screws B is Rs 10. Therefore, the constraints are
`4x+6y <= 240`
`6x + 3y < 240`
Total profit, Z = 7x + 10y
The mathematical formulation of the given problem is
Maximize Z = 7x + 10y … (1)
subject to the constraints,
`4x+6y <=240`… (2)
`6x +3y <= 240` … (3)
x, y ≥ 0 … (4)
The feasible region determined by the system of constraints is
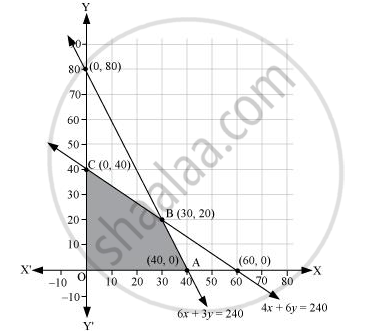
The corner points are A (40, 0), B (30, 20), and C (0, 40).
The values of Z at these corner points are as follows.
| Corner point | Z = 7x + 10y | |
| A(40, 0) | 280 | |
| B(30, 20) | 410 | → Maximum |
| C(0, 40) | 400 |
The maximum value of Z is 410 at (30, 20).
Thus, the factory should produce 30 packages of screws A and 20 packages of screws B to get the maximum profit of Rs 410.
APPEARS IN
RELATED QUESTIONS
A diet of a sick person must contain at least 48 units of vitamin A and 64 units of vitamin B. Two foods F 1 and F2 are available. Food F1 costs Rs. 6 per unit and food F2 costs Rs. 10 per unit. One unit of food F1 contains 6 units of vitamin A and 7 units of vitamin B. One unit of food F2 contains 8 units of vitamin A and 12 units of vitamin B.Find the minimum cost for the diet that consists of mixture of these two foods and also meeting the minimal nutritional requirements.
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60/kg and Food Q costs Rs 80/kg. Food P contains 3 units /kg of vitamin A and 5 units /kg of vitamin B while food Q contains 4 units /kg of vitamin A and 2 units /kg of vitamin B. Determine the minimum cost of the mixture?
One kind of cake requires 200g flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftsman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftsman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time.
What number of rackets and bats must be made if the factory is to work at full capacity?
A manufacturer produces nuts ad bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit, of Rs 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 12 hours a day?
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours of assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2are available. Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit. One unit of food F1contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements?
Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal (in Rs) | ||
| From/To | A | B |
| D | 6 | 4 |
| E | 3 | 2 |
| F | 2.50 | 3 |
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to minimize the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
| kg per bag | ||
| Brand P | Brand Q | |
| Nitrogen | 3 | 3.5 |
| Phosphoric acid | 1 | 2 |
| Potash | 3 | 1.5 |
| Chlorine | 1.5 | 2 |
Refer to question 8. If the grower wants to maximize the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs 12 and Rs 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximize the profit?
A factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on the hand-operated machines to manufacture a packet of screws 'A' while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a packet of screws 'B'. Each machine is available for at most 4 hours on any day. The manufacturer can sell a packet of screws 'A' at a profit of 70 paise and screws 'B' at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit? Formulate the above LPP and solve it graphically and find the maximum profit.
A company sells two different products A and B. The two products are produced in a common production process and are sold in two different markets. The production process has a total capacity of 45000 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of units of A that can be sold is 7000 and that of B is 10,000. If the profit is Rs 60 per unit for the product A and Rs 40 per unit for the product B, how many units of each product should be sold to maximize profit? Formulate the problem as LPP.
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of ₹ 12 and ₹ 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximise the profit?
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 35 per package of nuts and ₹ 14 per package of bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates each machine for almost 12 hours a day? convert it into an LPP and solve graphically.
In a LPP, the linear function which has to be maximised or minimised is called a linear ______ function.
A manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is Rs 50 and that on type B circuit is Rs 60, formulate this problem as a LPP so that the manufacturer can maximise his profit.
A firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is Rs 400 and each small van is Rs 200. Not more than Rs 3000 is to be spent on the job and the number of large vans can not exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours. On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
A company manufactures two types of sweaters : type A and type B. It costs Rs 360 to make a type A sweater and Rs 120 to make a type B sweater. The company can make at most 300 sweaters and spend at most Rs 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of Rs 200 for each sweater of type A and Rs 120 for every sweater of type B.
Formulate this problem as a LPP to maximise the profit to the company.
Refer to question 11. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximise his profit? Determine the maximum profit.
Which of the following types of problems cannot be solved by linear programming methods?
Maximize Z = 11 x + 8y subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0.
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake require 100 g of flour and 50 kg fat. Find the mamximum number of cake which can be made from 5 kg of flour and l kg of fat assuming that there is no shortage of the other ingradients used in making the cakes.
