Advertisements
Advertisements
Question
A hollow metallic sphere is 2 cm thick all around and has an external diameter of 12 cm. Find the radius of the solid sphere made by recasting this hollow sphere.
Solution
External diameter of hollow sphere = 12 cm
External radius = R = 6 cm
Internal diameter of hollow sphere = ( 12 - 4) cm= 8 cm
Internal radius = r = 4 cm
Volume of metal used = `4/3pi(R^3 - r^3)`
= `4/3 xx 22/7 xx (6^3 - 4^3)`
= `4/3 xx 22/7 xx 152`
= 636.95 `"cm"^3`
Volume of metal used = 636.95 cm3 = volume of sdid sphere
⇒ `4/3pir^3 = 636.95`
⇒ `4/3 xx 22/7 xx r^3 = 636.95`
⇒ `r^3 = (636.95 xx 3 xx 7)/(4 xx 22)`
⇒ `r^3 = 151.99 = 152`
⇒ r = 5.34 cm
Radius of the solid sphere = 5.34 cm
APPEARS IN
RELATED QUESTIONS
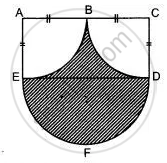
In the given figure, ABCD is the square of side 21 cm. AC and BD are two diagonals of the square. Two semicircles are drawn with AD and BC as diameters. Find the area of the shaded region. (Take `pi = 22/7`)

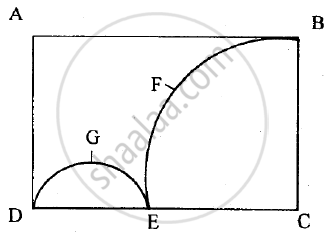
In the figure given below, ABCD is the rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle. (Take `pi = 22/7`).
Find the area of the biggest circle that can be cut from a rectangular piece of 44cm by 28 cm. Also, find the area of the paper left after cutting out the circle.
A circular hall, surmounted by a hemispherical roof, contains 5236 m3 of air. If the internal diameter of the room is equal to the height of the highest point of the roof from the floor, find the height of the hall.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
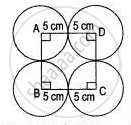
Four equal circles, each of radius 5 cm, touch each other as shown in the figure. Find the area included between them. (Take π= 3.14)
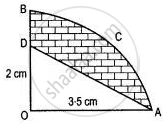
In the figure alongside, OAB is a quadrant of a circle. The radius OA = 3.5 cm and OD = 2 cm. Calculate the area of the shaded 22 portions.
The diagram represents the area swept by wiper of a car. With the dimension given in figure, calculate the shaded swept by the wiper.

AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take π = 3.14).
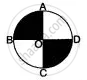
Calculate the area of the shaded region, if the diameter of the semi-circle is equal to 14 cm. (Take π = 22/7).