Advertisements
Advertisements
Question
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K–1, 1 atm. = 1.013 × 105 Pa; the membrane tension is 5 Nm–1.)
Solution
The pressure inside `P_i` balloon is larger than the outer pressure `P_a` of the atmosphere.
∴ `P_c = P_a = (2σ)/R`
σ = surface tension in the membrane of balloon R = radius of the balloon.
Gas or air inside is perfect (considered)
∴ `PV = n_iRT_i`
`V` = volume of the balloon
`n_c` = no. of moles of gas in the balloon
`R` = gas constant
`T_i` = temperature of balloon
`n_i = (PV)/(RT_i) = "mass of balloon (M)"/("molecular mass" (M_A))`
`n_i = M_1/M_A = (PV)/(RT_i)`
Similarly, `n_a = (P_aV)/(RT_a)`
By principal off floatation `W + M, g = Mσg`
W = weight lifted by balloon `W = M_ag - M_ig`
W = `(M_a - M_i)g`
Where `n_a` = no. of molecules of air displaced by balloon.
V = volume of air displaced by balloon equal to the volume of balloon If `M_a` mass of air displaced by the balloon
`M_A` = molecular mass inside or outside the balloon
∴ `n_σ = M_a/M_A`
`n_o = M_a/M_A = (P_oV)/(RT_a)`
⇒ `M_a = (P_aVM_A)/(RT_o)`
From (i), `M_i = (P_iVM_A)/(RT_i)`
W = `((P_0VM_A)/(RT_a) - (PVM_A)/(RT_i))g`
w = `(VM_A)/R (P_a/T_a - P_c/T_i)g`
`M_A = 21%` of `O_2 + 79%` of `N_2`
`M_A = 0.21 xx 32 + 0.79 xx 28`
`M_A = 4(0.21 xx 8 + 0.79 xx 7)`
`M_A = 4(1.68 + 5.53)`
`M_A = 4(7.21)`
`M_A = 28.84 g`
`M_A = 0.2884 kg`
`P_i = P_σ + (2σ)/R`
W = `4/3 pi xx 8 xx 8 xx 8 xx 0.2884`
= `[(1.013 xx 10^5)/(273 + 20) - P_i/(273 + 60)]g`
`P_i = P_a + P = P_a + (2σ)/R`
`P_i = [1.013 xx 10^5 + (2 xx 5)/8] = 101300 + 1.25`
`P_i = 101301.25 = 1.0130125 xx 10^5 = 1.013 xx 10^5`
∴ W = `(4 xx 3.14 xx 8 xx 8 xx 8 xx 0.02884)/(3 xx 8.314) [(1.013 xx 10^5)/293 - (1.013 xx 10^5)/333]g`
W = `(4 xx 3.14 xx 8 xx 8 xx 8 xx 0.02884 xx 1.013 xx 10^5)/(3 xx 8.314) [1/293 -1/333]g`
W = `(4 xx 3.14 xx 8 xx 8 xx 8 xx 0.02884 xx 1.013 xx 10^5 xx 9.8)/(3 xx 8.314) [1/293 -1/333]`
W =
`(4 xx 3.14 xx 8 xx 8 xx 8 xx 0.02884 xx 1.013 xx 10^5 xx 9.8 xx 40)/(3 xx 8.314)`
= 3044.2 N
APPEARS IN
RELATED QUESTIONS
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
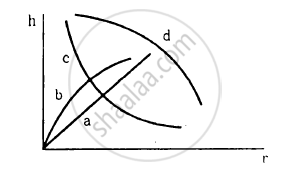
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
Under isothermal conditions, two soap bubbles of radii 'r1' and 'r2' coalesce to form a big drop. The radius of the big drop is ______.
Soap solution is used for cleaning dirty clothes because ______.
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
A coaxial cylinder made of glass is immersed in liquid of surface tension ' S'. Radius of inner and outer surface of cylinder are R1 and R2 respectively. Height till which liquid will rise is (Density of liquid is p):
