Advertisements
Advertisements
Question
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Solution
Given:
R = 0.2 cm,
n = 8,
T = 435.5 dyn/cm
To find:
The work done
Solution:
As the volume of the liquid remains constant, volume of n droplets = volume of the drop
∴ `"n"xx4/3pi"r"^3 = 4/3pi"R"^3`
∴ `"r"^3 = "R"^3/"n"`
∴ r = `"R"/root(3)("n") = "R"/root(3)(8) = "R"/2`
Surface area of the drop = 4πR2
Surface area of n droplets = n × 4πr2
∴ The increase in the surface area = surface area of n droplets – surface area of drop
= n × 4πr2 - 4πR2
= 4π(nr2 - R2)
= `4π(8xx"R"^2/4 - "R"^2)`
= 4π(2 - 1)R2 = 4πR2
∴ The work done = surface tension × increase in surface area
= T × 4πR2 = 435.5 × 4 × 3.142 × (0.2)2
= 2.189 × 10-5 J
APPEARS IN
RELATED QUESTIONS
Derive an expression for excess pressure inside a drop of liquid.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
Explain why Surface tension of a liquid is independent of the area of the surface
Explain why A drop of liquid under no external forces is always spherical in shape
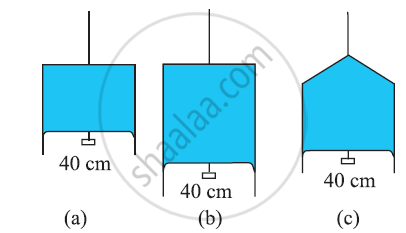
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
The total free surface energy of a liquid drop is `pisqrt2` times the surface tension of the liquid. Calculate the diameter of the drop in S.l. unit.
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
State any two characteristics of the angle of contact
When a sparingly soluble substance like alcohol is dissolved in water, surface tension of water
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?
An ice cube is suspended in vacuum in a gravity free hall. As the ice melts it
Air is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution in S, the work done in the process is
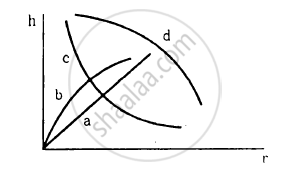
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
Find the excess pressure inside (a) a drop of mercury of radius 2 mm (b) a soap bubble of radius 4 mm and (c) an air bubble of radius 4 mm formed inside a tank of water. Surface tension of mercury, soap solution and water are 0.465 N m−1, 0.03 N m−1 and 0.076 N m−1 respectively.
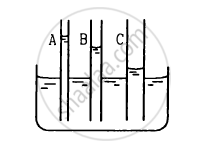
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.075 J m−2.
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J m−2.
Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water = 0.075 Nm−1.
A metal piece of mass 160 g lies in equilibrium inside a glass of water. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg/m3, find the normal force exerted by the bottom of the glass on the metal piece.

A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
Explain the capillary action.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
The water droplets are spherical in free fall due to ______
The surface tension of a liquid at critical temperature is ______
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Explain the phenomena of surface tension on the basis of molecular theory.
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
How does surface tension help a plant?
Describe an experiment to prove that friction depends on the nature of a surface.
Define the angle of contact for a given pair of solid and liquid.
Distinguish between cohesive and adhesive forces.
What is capillarity?
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
The wear and tear in the machine part is due to ______.
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
When one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of capillary is ______.
(Surface tension of water = 7 × 10-2 N/m)
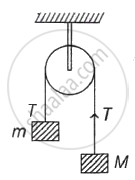
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
