Advertisements
Advertisements
प्रश्न
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
उत्तर
Given:
R = 0.2 cm,
n = 8,
T = 435.5 dyn/cm
To find:
The work done
Solution:
As the volume of the liquid remains constant, volume of n droplets = volume of the drop
∴ `"n"xx4/3pi"r"^3 = 4/3pi"R"^3`
∴ `"r"^3 = "R"^3/"n"`
∴ r = `"R"/root(3)("n") = "R"/root(3)(8) = "R"/2`
Surface area of the drop = 4πR2
Surface area of n droplets = n × 4πr2
∴ The increase in the surface area = surface area of n droplets – surface area of drop
= n × 4πr2 - 4πR2
= 4π(nr2 - R2)
= `4π(8xx"R"^2/4 - "R"^2)`
= 4π(2 - 1)R2 = 4πR2
∴ The work done = surface tension × increase in surface area
= T × 4πR2 = 435.5 × 4 × 3.142 × (0.2)2
= 2.189 × 10-5 J
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Angle of contact for the pair of pure water with clean glass is _______.
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
The total free surface energy of a liquid drop is `pisqrt2` times the surface tension of the liquid. Calculate the diameter of the drop in S.l. unit.
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
When a sparingly soluble substance like alcohol is dissolved in water, surface tension of water
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
By a surface of a liquid we mean
Air is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution in S, the work done in the process is
If two soap bubbles of different radii are connected by a tube,
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
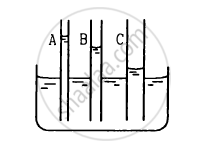
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.075 J m−2.
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension the the thread. Surface tension of soap solution = 0.030 N m−1.
A metal piece of mass 160 g lies in equilibrium inside a glass of water. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg/m3, find the normal force exerted by the bottom of the glass on the metal piece.

A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. Water can be the minimum edge of the block so that it does not sink in water? Specific gravity of ice = 0.9.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly ______.
Insect moves over the surface of water because of ______.
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
How does the friction arise between the surfaces of two bodies in relative motion?
Explain elasticity using intermolecular forces.
Distinguish between cohesive and adhesive forces.
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
Obtain an expression for the surface tension of a liquid by the capillary rise method.
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
A square frame of each side L is dipped in a soap solution and taken out. The force acting on the film formed is _____.
(T = surface tension of soap solution).
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
What is surface tension? Explain the applications of surface tension.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
A soap bubble of radius 3 cm is formed inside another soap bubble of radius 6 cm. The radius of an equivalent soap bubble which has the same excess pressure as inside the smaller bubble with respect to the atmospheric pressure is ______ cm.
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
The surface tension of a soap solution is T. The work done in blowing a soap bubble of diameter d to that of a diameter 2d is ______.
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
Define angle of contact.
