Advertisements
Advertisements
प्रश्न
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
उत्तर
Let diameter of capillary tube = d mm
Let the radius of capillary tube r1 = r mm
Capillary rise h1 = 30 mm
Let the radius of another capillary tube r2 = `2/3` r
Let the capillary rise of another capillary tube be h2
We know that
T = `("hr"ρ"g")/2`
∴ `"h" ∝ 1/"r"`
`"h"_1/"h"_2 = "r"_2/"r"_1`
`30/"h"_2 = (2/3 "r")/"r"`
`30/"h"_2 = 2/3`
∴ h2 = `(3 xx 30)/2` = 45 mm
Capillary rise in the new capillary tube = 45 mm
APPEARS IN
संबंधित प्रश्न
State any two characteristics of the angle of contact
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
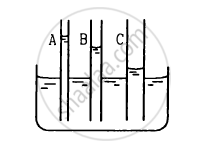
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
The surface tension of soap solution is 25 × 10-3 Nm-1. The excess of pressure inside a soap bubble of diameter 1 cm is ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
