Advertisements
Advertisements
प्रश्न
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
उत्तर
Given:
Length of the edge of the metal block, x = 12 cm
Specific gravity of mercury, \[\rho_{Hg}\]= 13.6 gm/cc
It is given that`1/5`th of the cubical block is inside mercury initially.
Let `rho_b` be the density of the block in gm/cc.
\[\therefore (\text{ x } )^3 \times \rho_\text{ b } \times \text{ g } = (\text{ x } )^2 \times \left( \frac{\text{x}}{5} \right) \times \rho_{Hg} \times \text{g}\]
\[ \Rightarrow (12 )^3 \times \rho_\text{b} \times \text{g} = (12 )^2 \times \frac{12}{5} \times 13 . 6\]
\[ \Rightarrow \rho_\text{ b } = \frac{13 . 6}{5} \text{ gm/cc }\]
Let y be the height of the water column after the water is poured.
∴ Vb = VHg + Vw = (12)3
Here,
VHg = Volume of the block inside mercury
Vw = Volume of the block inside water
\[\therefore ( \text {V}_\text{b} \times \rho_\text{b} \times \text{g}) = ( \text{V}_{\text{Hg}} \times \rho_{\text{Hg}} \times \text{g}) + ( \text{V}_\text{w} \times \rho_\text{w} \times \text{g})\]
\[ \Rightarrow ( \text{V}_{\text{Hg}} + \text{V}_\text{w} ) \times \frac{13 . 6}{5} = \text{V}_{\text{Hg}} \times 13 . 6 + \text{V}_\text{w} \times 1\]
\[ \Rightarrow (12 )^3 \times \frac{13 . 6}{5} = (12 - \text{y}) \times (12 )^2 \times 13 . 6 + (\text{y}) \times (12 )^2 \times 1\]
\[ \Rightarrow 12 \times \frac{13 . 6}{5} = (12 -\text{ y}) \times 13 . 6 + (\text{y})\]
\[ \Rightarrow 12 . 6\text{y }= 13 . 6\left( 12 - \frac{12}{5} \right) = (13 . 6) \times (9 . 6)\]
\[ \Rightarrow \text{y} = \frac{(9 . 6) \times (13 . 6)}{(12 . 6)} = 10 . 4 \text{cm}\]
APPEARS IN
संबंधित प्रश्न
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
The surface tension of water at 0ºc is 75·5 dyne/cm. Find surface tension of water at 25°C. [ α for water = 0·0021/°C ]
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Explain why A drop of liquid under no external forces is always spherical in shape
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
Define surface tension and surface energy.
If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?
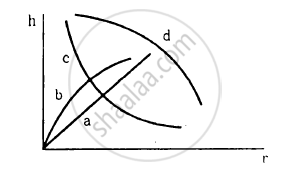
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
Describe an experiment to prove that friction depends on the nature of a surface.
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
A square frame of each side L is dipped in a soap solution and taken out. The force acting on the film formed is _____.
(T = surface tension of soap solution).
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
Under isothermal conditions, two soap bubbles of radii 'r1' and 'r2' coalesce to form a big drop. The radius of the big drop is ______.
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K–1, 1 atm. = 1.013 × 105 Pa; the membrane tension is 5 Nm–1.)
When one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of capillary is ______.
(Surface tension of water = 7 × 10-2 N/m)
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
