Advertisements
Advertisements
प्रश्न
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
उत्तर
Given:
Length of the edge of the metal block, x = 12 cm
Specific gravity of mercury, \[\rho_{Hg}\]= 13.6 gm/cc
It is given that`1/5`th of the cubical block is inside mercury initially.
Let `rho_b` be the density of the block in gm/cc.
\[\therefore (\text{ x } )^3 \times \rho_\text{ b } \times \text{ g } = (\text{ x } )^2 \times \left( \frac{\text{x}}{5} \right) \times \rho_{Hg} \times \text{g}\]
\[ \Rightarrow (12 )^3 \times \rho_\text{b} \times \text{g} = (12 )^2 \times \frac{12}{5} \times 13 . 6\]
\[ \Rightarrow \rho_\text{ b } = \frac{13 . 6}{5} \text{ gm/cc }\]
Let y be the height of the water column after the water is poured.
∴ Vb = VHg + Vw = (12)3
Here,
VHg = Volume of the block inside mercury
Vw = Volume of the block inside water
\[\therefore ( \text {V}_\text{b} \times \rho_\text{b} \times \text{g}) = ( \text{V}_{\text{Hg}} \times \rho_{\text{Hg}} \times \text{g}) + ( \text{V}_\text{w} \times \rho_\text{w} \times \text{g})\]
\[ \Rightarrow ( \text{V}_{\text{Hg}} + \text{V}_\text{w} ) \times \frac{13 . 6}{5} = \text{V}_{\text{Hg}} \times 13 . 6 + \text{V}_\text{w} \times 1\]
\[ \Rightarrow (12 )^3 \times \frac{13 . 6}{5} = (12 - \text{y}) \times (12 )^2 \times 13 . 6 + (\text{y}) \times (12 )^2 \times 1\]
\[ \Rightarrow 12 \times \frac{13 . 6}{5} = (12 -\text{ y}) \times 13 . 6 + (\text{y})\]
\[ \Rightarrow 12 . 6\text{y }= 13 . 6\left( 12 - \frac{12}{5} \right) = (13 . 6) \times (9 . 6)\]
\[ \Rightarrow \text{y} = \frac{(9 . 6) \times (13 . 6)}{(12 . 6)} = 10 . 4 \text{cm}\]
APPEARS IN
संबंधित प्रश्न
Angle of contact for the pair of pure water with clean glass is _______.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
The surface tension of water at 0ºc is 75·5 dyne/cm. Find surface tension of water at 25°C. [ α for water = 0·0021/°C ]
Explain why Surface tension of a liquid is independent of the area of the surface
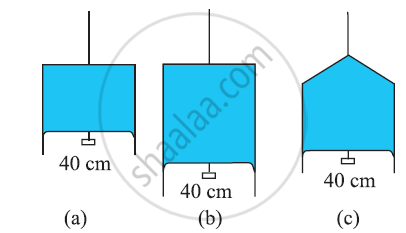
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. Water can be the minimum edge of the block so that it does not sink in water? Specific gravity of ice = 0.9.
A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
Explain the capillary action.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
What is capillarity?
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
When one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of capillary is ______.
(Surface tension of water = 7 × 10-2 N/m)
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
