Advertisements
Advertisements
प्रश्न
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
उत्तर
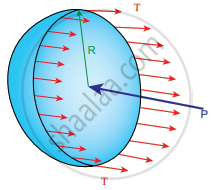
i. Excess of pressure inside air bubble in a liquid: Consider an air bubble of radius R inside a liquid having surface tension T. Let P1 and P2 be the pressures outside and inside the air bubble, respectively.
Now, the excess pressure inside the air bubble is ∆P = P1 – P2
Air bubble
In order to find the excess pressure inside the air bubble, let us consider the forces acting on the air bubble. For the hemispherical portion of the bubble, considering the forces acting on it, we get,
- The force due to surface tension acting towards right around the rim of length 2πR is FT = 2πRT
- The force due to outside pressure P, is to the right acting across a cross-sectional area of πR2 is `"P"_1π"R"^2`
- The force due to pressure P2 inside the bubble, acting to the left is `"F"_("P"_2) = "P"_2π"R"^2`
As the air bubble is in equilibrium under the action of these forces, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
Excess pressure is ∆P = P2 – P1 = `(2"T")/"R"`
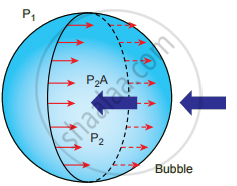
ii. Excess pressure inside a soap bubble: Consider a soap bubble of radius R and the surface tension of the soap bubble be T. A soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble. Therefore, the force on the soap bubble due to surface tension is 2 × 2πRT.
Soap bubble
The various forces acting on the soap bubble are,
- Force due to surface tension FT = 4πRT towards right.
- Force due to outside pressure, `"F"_("P"_1) = "P"_1π"R"^2` towards right
- Force due to inside pressure, `"F"_("P"_2) = "P"_2π"R"^2` towards left
As the bubble is in equilibrium, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
P2πR2 = 4πRT + P1πR2 ⇒ (P2 − P1)πR2 = 4πPT
Excess pressure is ∆P = P2 – P1 = `(4"T")/"R"`
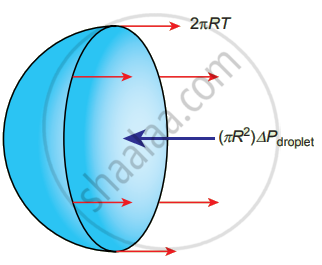
iii. Excess pressure inside the liquid drop: Consider a liquid drop of radius R and the surface tension of the liquid is T.
Liquid drop
The various forces acting on the liquid drop are,
- Force due to surface tension FT = 2πRT towards right
- Force due to outside pressure, `"F"_("P"_1) = "P"_1π"R"^2` towards right
- Force due to inside pressure, `"F"_("P"_2) = "P"_2π"R"^2` towards left
As the drop is in equilibrium, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
P2πR2 = 2πRT + P1πR2 ⇒ (P2 − P1)πR2 = 2πPT
Excess pressure is ∆P = P2 – P1 = `(2"T")/"R"`
APPEARS IN
संबंधित प्रश्न
Derive an expression for excess pressure inside a drop of liquid.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
Explain why Water with detergent dissolved in it should have small angles of contact.
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
When water droplets merge to form a bigger drop
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
A water drop of radius R' splits into 'n' smaller drops, each of radius 'r'. The work done in the process is ______.
T = surface tension of water
A coaxial cylinder made of glass is immersed in liquid of surface tension ' S'. Radius of inner and outer surface of cylinder are R1 and R2 respectively. Height till which liquid will rise is (Density of liquid is p):
