Advertisements
Advertisements
प्रश्न
Derive an expression for excess pressure inside a drop of liquid.
उत्तर
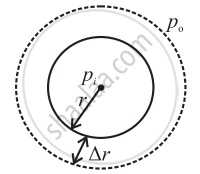
Consider a spherical drop as shown in the figure. Let pi be the pressure inside the drop and p0 be the pressure out side it. As the drop is spherical in shape, the pressure, pi, inside the drop is greater than p0, the pressure outside. Therefore, the excess pressure inside the drop is pi - p0.
Let the radius of the drop increase from r to r + ∆r, where ∆r is very small, so that the pressure inside the drop remains almost constant.
Let the initial surface area of the drop be A1 = 4πr2 , and the final surface area of the drop be A2 = 4π (r+∆r)2.
∴ A2 = 4π(r2 + 2r∆r + ∆r2)
∴ A2 = 4πr2 + 8πr∆r + 4π∆r2 (As ∆r is very small, ∆r2 can be neglected)
∴ A2 = 4πr2 + 8πr∆r
Thus, increase in the surface area of the drop is
`dA = A_2 – A_1 = 8πrDeltar`
Work done in increasing the surface area by `dA` is stored as excess surface energy.
`therefore dW = TdA= T (8πrDeltar)` ... (1)
This work done is also equal to the product of the force F which causes increase in the area of the drop and the displacement ∆r which is the increase in the radius of the bubble.
`therefore dW = F∆r` ... (2)
The excess force is given by,
(Excess pressure) ×(Surface area)
∴ F = (pi – p0) 4πr2 ... (3)
Equating Eq. (1), and Eq. (2), we get,
`T(8πrDeltar) = FDeltar`
`therefore T(8πrDeltar) = (p_i – p_0) 4πr^2Deltar` ... (using Eq. (3))
`therefore (p_i – p_0)=(2T)/r`
This equation gives the excess pressure inside a drop of liquid.
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
Draw a neat labelled diagram showing forces acting on the meniscus of water in a capillary tube.
'n' droplets of equal size of radius r coalesce to form a bigger drop of radius R. The energy liberated is equal to...................
(T =Surface tension of water)
`(a) 4piR^2T[n^(1/3)-1]`
`(b) 4pir^2T[n^(1/3)-1]`
`(c) 4piR^2T[n^(2/3)-1]`
`(d)4 pir^2T[n^(2/3)-1]`
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Explain why Surface tension of a liquid is independent of the area of the surface
Explain why A drop of liquid under no external forces is always spherical in shape
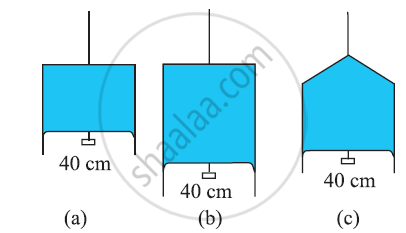
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
The total free surface energy of a liquid drop is `pisqrt2` times the surface tension of the liquid. Calculate the diameter of the drop in S.l. unit.
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of soap solution is 30 dyne/cm. (Π = 3.142).
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
If a mosquito is dipped into water and released, it is not able to fly till it is dry again. Explain
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
By a surface of a liquid we mean
If more air is pushed in a soap bubble, the pressure in it
If two soap bubbles of different radii are connected by a tube,
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
The properties of a surface are different from those of the bulk liquid because the surface molecules
(a) are smaller than other molecules
(b) acquire charge due to collision from air molecules
(c) find different type of molecules in their range of influence
(d) feel a net force in one direction.
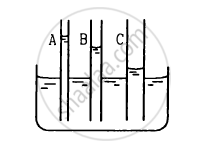
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water = 0.075 Nm−1.
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension the the thread. Surface tension of soap solution = 0.030 N m−1.
A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
A hollow spherical body of inner and outer radii 6 cm and 8 cm respectively floats half-submerged in water. Find the density of the material of the sphere.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
The surface tension of a liquid at critical temperature is ______
Define surface tension
What will be the shape of the liquid meniscus for the obtuse angle of contact?
The property of _______ of a liquid surface enables the water droplets to move upward in plants.
The wettability of a surface by a liquid depends primarily on
Define the surface tension of a liquid.
Mention the S.I unit and dimension of surface tension.
Define the angle of contact for a given pair of solid and liquid.
Distinguish between cohesive and adhesive forces.
Obtain an expression for the surface tension of a liquid by the capillary rise method.
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
A square frame of each side L is dipped in a soap solution and taken out. The force acting on the film formed is _____.
(T = surface tension of soap solution).
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
Under isothermal conditions, two soap bubbles of radii 'r1' and 'r2' coalesce to form a big drop. The radius of the big drop is ______.
The wear and tear in the machine part is due to ______.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
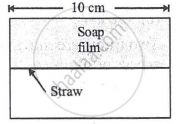
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Work done to blow a bubble of volume V is W. The work done in blowing a bubble of volume 2V will be ______.
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
