Advertisements
Advertisements
प्रश्न
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Advertisements
उत्तर १
The angle between the tangent to the liquid surface at the point of contact and the surface inside the liquid is called the angle of contact (θ), as shown in the given figure.
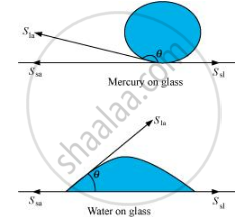
Sla, Ssa, and Ssl are the respective interfacial tensions between the liquid-air, solid-air, and solid-liquid interfaces. At the line of contact, the surface forces between the three media must be in equilibrium, i.e.,
`cos theta = (S_(sa) - S_(sl))/S_(la)`
The angle of contact θ , is obtuse if Ssa < Sla (as in the case of mercury on glass). This angle is acute if Ssl < Sla (as in the case of water on glass).
उत्तर २
Let a drop of a liquid L be poured on a solid surface S placed in air A. If TSL,and TSA be the surface tensions corresponding to solid-liquid layer, liquid-air layer and solid-air layer respectively and θ be the angle of contact between the liquid and solid ,then
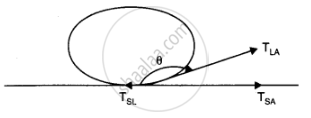
TLA Cos θ + TSL =TSA
=>Cos θ=TSA-TSL/TLA
For the mercury-glass interface, TSA< TSL.
Therefore, cos 0 is negative. Thus θ is an obtuse angle. For the water-glass interface, TSA > TSL. Therefore cos 0 is positive. Thus, θ is an acute angle.
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Angle of contact for the pair of pure water with clean glass is _______.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
The total free surface energy of a liquid drop is `pisqrt2` times the surface tension of the liquid. Calculate the diameter of the drop in S.l. unit.
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
If a mosquito is dipped into water and released, it is not able to fly till it is dry again. Explain
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
Why is the surface tension of paints and lubricating oils kept low?
Explain the capillary action.
What will be the shape of the liquid meniscus for the obtuse angle of contact?
A u-tube is made up of capillaries of bore 1 mm and 2 mm respectively. The tube is held vertically and partially filled with a liquid of surface tension 49 dyne/cm and zero angles of contact. Calculate the density of the liquid, if the difference in the levels of the meniscus is 1.25 cm. take g = 980 cm/s2
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
The surface tension of boiling water is ______.
