Advertisements
Advertisements
प्रश्न
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
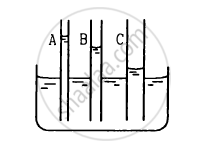
उत्तर
Given:
Surface tension of water T = 7.5 × 10−2 N/m
Taking cos θ = 1:
Radius of capillary A (rA) = 0.5 mm = 0.5 × 10−3 m
Height of water level in capillary A:
\[\text{h}_\text{A } = \frac{2\text{T} \cos \theta}{\text{r}_\text{A} \rho \text{ g}}\]
\[ = \frac{2 \times 7 . 5 \times {10}^{- 2}}{0 . 5 \times {10}^{- 3} \times 1000 \times 10}\]
\[ = 3 \times {10}^{- 2}\text{ m = 3 cm}\]
Radius of capillary B (rB) = 1 mm = 1 × 10−3 m
Height of water level in capillary B:
\[\text{h}_\text{B} = \frac{2\text{T}\cos \theta}{\text{r}_\text{B} \rho \text{ g}}\]
\[ = \frac{2 \times 7 . 5 \times {10}^{- 2}}{1 \times {10}^{- 3} \times {10}^3 \times 10}\]
\[ = 15 \times {10}^{- 3} \text{ m = 1 . 5 cm }\]
Radius of capillary C (rC) = 1.5 mm = 1.5 × 10−3 m
Height of water level in capillary C:
\[\text{h}_\text{C} = \frac{2\text{T} \cos \theta}{\text{r}_\text{ C} \rho \text{ g}}\]
\[ = \frac{2 \times 7 . 5 \times {10}^{- 2}}{1 . 5 \times {10}^{- 3} \times {10}^3 \times 10}\]
\[ = \frac{15}{1 . 5} \times {10}^{- 3} \text{ m = 1 cm} \]
APPEARS IN
संबंधित प्रश्न
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Explain why Water with detergent dissolved in it should have small angles of contact.
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
A uniform vertical tube of circular cross section contains a liquid. The contact angle is 90°. Consider a diameter of the tube lying in the surface of the liquid. The surface to the right of this diameter pulls the surface on the left of it. What keeps the surface on the left in equilibrium?
A 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water = 0.076 N m−1.
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
The lower end of a capillary tube of radius 1 mm is dipped vertically into mercury. (a) Find the depression of mercury column in the capillary. (b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertical. Surface tension of mercury = 0.465 N m−1 and the contact angle of mercury with glass −135 °.
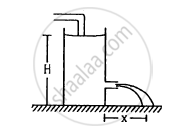
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
Two soap bubbles have a radius in the ratio of 2:3. Compare the works done in blowing these bubbles.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
How is surface tension related to surface energy?
A square frame of each side L is dipped in a soap solution and taken out. The force acting on the film formed is _____.
(T = surface tension of soap solution).
The wear and tear in the machine part is due to ______.
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
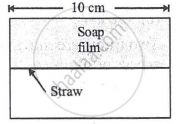
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
The surface tension of soap solution is 25 × 10-3 Nm-1. The excess of pressure inside a soap bubble of diameter 1 cm is ______.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
