Advertisements
Advertisements
Question
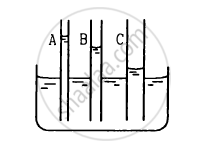
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
Solution
Given:
Surface tension of water T = 7.5 × 10−2 N/m
Taking cos θ = 1:
Radius of capillary A (rA) = 0.5 mm = 0.5 × 10−3 m
Height of water level in capillary A:
\[\text{h}_\text{A } = \frac{2\text{T} \cos \theta}{\text{r}_\text{A} \rho \text{ g}}\]
\[ = \frac{2 \times 7 . 5 \times {10}^{- 2}}{0 . 5 \times {10}^{- 3} \times 1000 \times 10}\]
\[ = 3 \times {10}^{- 2}\text{ m = 3 cm}\]
Radius of capillary B (rB) = 1 mm = 1 × 10−3 m
Height of water level in capillary B:
\[\text{h}_\text{B} = \frac{2\text{T}\cos \theta}{\text{r}_\text{B} \rho \text{ g}}\]
\[ = \frac{2 \times 7 . 5 \times {10}^{- 2}}{1 \times {10}^{- 3} \times {10}^3 \times 10}\]
\[ = 15 \times {10}^{- 3} \text{ m = 1 . 5 cm }\]
Radius of capillary C (rC) = 1.5 mm = 1.5 × 10−3 m
Height of water level in capillary C:
\[\text{h}_\text{C} = \frac{2\text{T} \cos \theta}{\text{r}_\text{ C} \rho \text{ g}}\]
\[ = \frac{2 \times 7 . 5 \times {10}^{- 2}}{1 . 5 \times {10}^{- 3} \times {10}^3 \times 10}\]
\[ = \frac{15}{1 . 5} \times {10}^{- 3} \text{ m = 1 cm} \]
APPEARS IN
RELATED QUESTIONS
The surface tension of water at 0°C is 75.5 dyne/cm. Calculate surface tension of water at 25°C.
(α for water = 2.7×10-3/°C)
Define surface tension and surface energy.
By a surface of a liquid we mean
If two soap bubbles of different radii are connected by a tube,
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
Explain the phenomena of surface tension on the basis of molecular theory.
How does surface tension help a plant?
Explain elasticity using intermolecular forces.
How is surface tension related to surface energy?
Define the angle of contact for a given pair of solid and liquid.
Is surface tension a vector?
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
A coaxial cylinder made of glass is immersed in liquid of surface tension ' S'. Radius of inner and outer surface of cylinder are R1 and R2 respectively. Height till which liquid will rise is (Density of liquid is p):
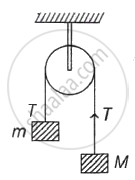
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
Define angle of contact.
