Advertisements
Advertisements
प्रश्न
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
उत्तर
Given:
Surface area of mercury drop, A = 1 mm2 = 10−6 m2
Radius of mercury drop, r = 4 mm = 4 × 10−3 m
Atmospheric pressure, P0 = 1.0 × 105 Pa
Surface tension of mercury, T = 0.465 N/m
(a) Force exerted by air on the surface area:
F = P0A
⇒ F= 1.0 × 105 × 10−6 = 0.1 N
(b) Force exerted by mercury below the surface area :
\[\text{ Pressure P' = P}_0 + \frac{2T}{\text{r}}\]
\[F = P'A = \left( P_0 + \frac{2T}{r} \right)A\]
\[ = \left( 0 . 1 + \frac{2 \times 0 . 465}{4 \times {10}^{- 3}} \right) \times {10}^{- 6} \]
\[ = 0 . 1 + 0 . 00023 = 0 . 10023 \text{N}\]
(c) Force exerted by mercury surface in contact with it:
\[P = \frac{2T}{r}\]
\[F = PA = \frac{2T}{r}A\]
\[ = \frac{2 \times 0 . 465}{4 \times {10}^{- 3}} \times {10}^{- 6} = 0 . 00023 \text{ N}\]
APPEARS IN
संबंधित प्रश्न
Fill in the blanks using the word(s) from the list appended with each statement
Surface tension of liquids generally . . . with temperatures (increases / decreases)
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
Viscosity is a property of
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension the the thread. Surface tension of soap solution = 0.030 N m−1.
A hollow spherical body of inner and outer radii 6 cm and 8 cm respectively floats half-submerged in water. Find the density of the material of the sphere.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
Why is the surface tension of paints and lubricating oils kept low?
Explain the capillary action.
How does the friction arise between the surfaces of two bodies in relative motion?
Explain elasticity using intermolecular forces.
What do you mean by capillarity or capillary action?
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K–1, 1 atm. = 1.013 × 105 Pa; the membrane tension is 5 Nm–1.)
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
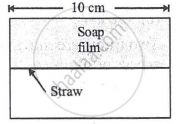
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
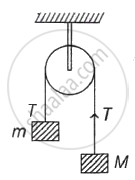
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Define angle of contact.
