Advertisements
Advertisements
प्रश्न
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
उत्तर
Given:
Radius of capillary tube r = 1 mm = 10−3 m
(a) Let T be the surface tension and ρ be the density of the liquid.
Then, for cos θ = 1, height (h) of liquid level:\[h = \frac{2T}{r\rho g}\] ........... (i),
where g is the acceleration due to gravity
\[\Rightarrow \text{ h } = \frac{2 \times \left( 0 . 076 \right)}{{10}^{- 3} \times 10 \times 100}\]
\[ = 1 . 52 \text{ cm} \]
\[ = 1 . 52 \times {10}^{- 2} \text{ m }\]
\[ = 1 . 52 \text{ cm }\]
(b) Let the new length of the tube be h'.
\[\text{ h }' = \frac{2T\cos \theta}{\text{ r }\rho \text{ g }}\]
\[\cos \theta = \frac{\text{ h'r }\rho g}{2T}\]
\[\text{ Using equation }\left( \text{ i } \right), \text{ we get: }\]
\[\cos \theta = \frac{h'}{h} = \frac{1}{2} \left( \text{ Because h' }= \frac{h}{2} \right)\]
\[ \Rightarrow \theta = \cos^{- 1} \left( \frac{1}{2} \right) = 60^\circ\]
The water surface in the capillary makes an angle of 60∘with the wall.
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Draw a neat labelled diagram showing forces acting on the meniscus of water in a capillary tube.
Define the angle of contact.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J m−2.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

A hollow spherical body of inner and outer radii 6 cm and 8 cm respectively floats half-submerged in water. Find the density of the material of the sphere.
The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly ______.
Why is the surface tension of paints and lubricating oils kept low?
Distinguish between cohesive and adhesive forces.
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
A soap bubble of radius 3 cm is formed inside another soap bubble of radius 6 cm. The radius of an equivalent soap bubble which has the same excess pressure as inside the smaller bubble with respect to the atmospheric pressure is ______ cm.
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
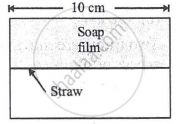
The surface tension of boiling water is ______.
