Advertisements
Advertisements
Question
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
Solution
Given:
Radius of capillary tube r = 1 mm = 10−3 m
(a) Let T be the surface tension and ρ be the density of the liquid.
Then, for cos θ = 1, height (h) of liquid level:\[h = \frac{2T}{r\rho g}\] ........... (i),
where g is the acceleration due to gravity
\[\Rightarrow \text{ h } = \frac{2 \times \left( 0 . 076 \right)}{{10}^{- 3} \times 10 \times 100}\]
\[ = 1 . 52 \text{ cm} \]
\[ = 1 . 52 \times {10}^{- 2} \text{ m }\]
\[ = 1 . 52 \text{ cm }\]
(b) Let the new length of the tube be h'.
\[\text{ h }' = \frac{2T\cos \theta}{\text{ r }\rho \text{ g }}\]
\[\cos \theta = \frac{\text{ h'r }\rho g}{2T}\]
\[\text{ Using equation }\left( \text{ i } \right), \text{ we get: }\]
\[\cos \theta = \frac{h'}{h} = \frac{1}{2} \left( \text{ Because h' }= \frac{h}{2} \right)\]
\[ \Rightarrow \theta = \cos^{- 1} \left( \frac{1}{2} \right) = 60^\circ\]
The water surface in the capillary makes an angle of 60∘with the wall.
APPEARS IN
RELATED QUESTIONS
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Explain why A drop of liquid under no external forces is always spherical in shape
The total free surface energy of a liquid drop is `pisqrt2` times the surface tension of the liquid. Calculate the diameter of the drop in S.l. unit.
When the size of a soap bubble is increased by pushing more air in it, the surface area increases. Does it mean that the average separation between the surface molecules is increased?
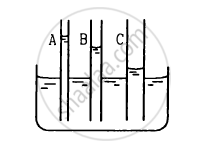
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
The lower end of a capillary tube of radius 1 mm is dipped vertically into mercury. (a) Find the depression of mercury column in the capillary. (b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertical. Surface tension of mercury = 0.465 N m−1 and the contact angle of mercury with glass −135 °.
Consider an ice cube of edge 1.0 cm kept in a gravity-free hall. Find the surface area of the water when the ice melts. Neglect the difference in densities of ice and water.
A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Obtain an expression for the capillary rise or fall using the forces method.
How does surface tension help a plant?
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
The wettability of a surface by a liquid depends primarily on
What is capillarity?
What is surface tension? Explain the applications of surface tension.
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
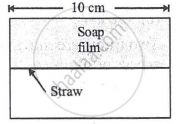
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
