Advertisements
Advertisements
Question
Obtain an expression for the capillary rise or fall using the forces method.
Solution
- When a glass capillary tube is dipped into a liquid, then the liquid rises in the capillary against gravity.
Hence, the weight of the liquid column must be equal and opposite to the component of force due to surface tension at the point of contact. - The length of liquid in contact inside the capillary is the circumference 2πr.
Let, r = radius of the capillary tube
h = height of liquid level in the tube
T = surface tension of the liquid
ρ = density of liquid
g = acceleration due to gravity
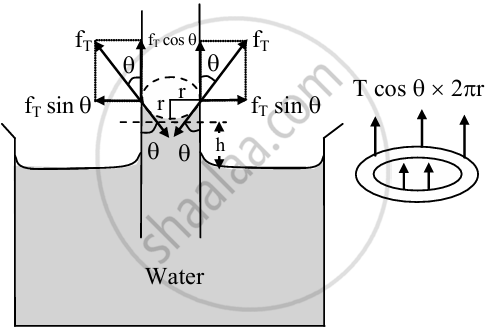
Rise of liquid in capillary tube - The force of magnitude fT acts tangentially on a unit length of liquid surface which is in contact with the wall of the capillary tube and is given as fT = T × 2πr
This force can be resolved into two components:
a. fT cosθ - vertically upward and
b. fT sinθ - along horizontal - The vertical component is effective. The horizontal component is not responsible for the capillary rise.
- The vertical component of force acting on the liquid column
(fT)v = force per unit length × circumference
= T cosθ × 2πr - Upward force balances the weight of the liquid in the capillary.
W = mg = Vρg = πr2hρg
where V = volume of liquid rise in the tube (ignoring the liquid in the concave meniscus.)
m = mass of the liquid in the capillary rise. This must be equal and opposite to the vertical component of the force due to surface tension. - If the liquid in the meniscus is neglected, then for equilibrium.,
2πr T cos θ = πr2 h ρg
∴ `h = (2T cos theta)/(r rho g )` ...(1) - This is the required expression for the rising or fall of liquid in a capillary tube.
RELATED QUESTIONS
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
Draw a neat labelled diagram showing forces acting on the meniscus of water in a capillary tube.
Explain why Surface tension of a liquid is independent of the area of the surface
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
The total energy of free surface of a liquid drop is 2π times the surface tension of the liquid. What is the diameter of the drop? (Assume all terms in SI unit).
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of soap solution is 30 dyne/cm. (Π = 3.142).
When a sparingly soluble substance like alcohol is dissolved in water, surface tension of water
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
By a surface of a liquid we mean
If two soap bubbles of different radii are connected by a tube,
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
The contact angle between a solid and a liquid is a property of
(a) the material of the solid
(b) the material of the liquid
(c) the shape of the solid
(d) the mass of the solid
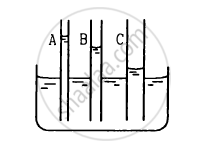
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water = 0.075 N m−1.
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension the the thread. Surface tension of soap solution = 0.030 N m−1.
A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
Why is the surface tension of paints and lubricating oils kept low?
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
Explain the phenomena of surface tension on the basis of molecular theory.
A u-tube is made up of capillaries of bore 1 mm and 2 mm respectively. The tube is held vertically and partially filled with a liquid of surface tension 49 dyne/cm and zero angles of contact. Calculate the density of the liquid, if the difference in the levels of the meniscus is 1.25 cm. take g = 980 cm/s2
How does surface tension help a plant?
Describe an experiment to prove that friction depends on the nature of a surface.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
The wettability of a surface by a liquid depends primarily on
What do you mean by capillarity or capillary action?
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
A molecule of water on the surface experiences a net ______.
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
What is surface tension? Explain the applications of surface tension.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
In a U-tube, the radii of two columns are respectively r1 and r2. When a liquid of density ρ(θ = 0°) is filled in it, a level difference of h is observed on two arms, then the surface tension of the liquid is ______.
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
The surface tension of boiling water is ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
Define angle of contact.
