Advertisements
Advertisements
Question
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
Solution
\[\text{ Height of the liquid in the capillary tube is given by }: \]
\[\text{ h } = \frac{2Scos\theta}{r\rho g}\]
\[\text{ h = Height }\]
\[\text{ S = Surface tension }\]
\[\text{ r = Inner radius of the tube }\]
\[\rho = \text{ Density of the liquid }\]
\[\text{ g = Acceleration due to gravity }\]
\[a) \theta \text{ and } \rho \text{ depend upon the material of the capillary tube and the liquid }. \]
\[b) \text{ h is dependent on the length of the tube . If the length is insufficient, then h will be low } . \]
\[d) \text{ r is the inner radius of the tube } .\]
APPEARS IN
RELATED QUESTIONS
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Derive an expression for excess pressure inside a drop of liquid.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
'n' droplets of equal size of radius r coalesce to form a bigger drop of radius R. The energy liberated is equal to...................
(T =Surface tension of water)
`(a) 4piR^2T[n^(1/3)-1]`
`(b) 4pir^2T[n^(1/3)-1]`
`(c) 4piR^2T[n^(2/3)-1]`
`(d)4 pir^2T[n^(2/3)-1]`
Explain why Surface tension of a liquid is independent of the area of the surface
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
The contact angle between water and glass is 0°. When water is poured in a glass to the maximum of its capacity, the water surface is convex upward. The angle of contact in such a situation is more than 90°. Explain.
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
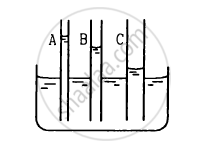
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
The property of _______ of a liquid surface enables the water droplets to move upward in plants.
What do you mean by capillarity or capillary action?
Why coffee runs up into a sugar lump (a small cube of sugar) when one corner of the sugar lump is held in the liquid?
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
A molecule of water on the surface experiences a net ______.
A water drop of radius R' splits into 'n' smaller drops, each of radius 'r'. The work done in the process is ______.
T = surface tension of water
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
