Advertisements
Advertisements
Questions
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Derive Laplace’s law for a spherical membrane.
Solution 1
Consider a spherical liquid drop and let the outside pressure be Po and inside pressure be Pi, such that the excess pressure is Pi − Po
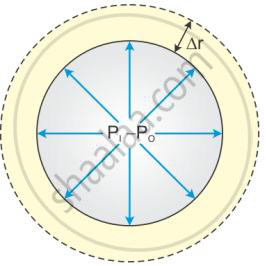
Let the radius of the drop increase from r to Δr, where Δr is very small, so that the pressure inside the drop remains almost constant.
Initial surface area (A1) = 4Πr2
Final surface area (A2) = 4Π(r + Δr)2
= 4π(r2 + 2rΔr + Δr2)
= 4Πr2 + 8ΠrΔr + 4ΠΔr2
As Δr is very small, Δr2 is neglected (i.e. 4πΔr2≅0)
Increase in surface area (dA) =A2 - A1= 4Πr2 + 8ΠrΔr - 4Πr2
Increase in surface area (dA) =8ΠΔr
Work done to increase the surface area by 8ΠrΔr is extra energy.
∴ dW = TdA
∴ dW = T*8πrΔr .......(Equ.1)
This work done is equal to the product of the force and the distance Δr.
dF=(P1 - P0)4πr2
The increase in the radius of the bubble is Δr.
dW = dFΔr = (P1 - P0)4Πr2*Δr ..........(Equ.2)
Comparing Equations 1 and 2, we get
(P1 - P0)4πr2*Δr = T*8πrΔr
∴`(P_1 - P_0) = (2T)/R`
This is called Laplace’s law of spherical membrane.
Solution 2
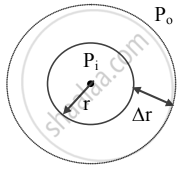
- The free surface of drops or bubbles is spherical in shape.
Let,
Pi = inside pressure of a drop or air bubble
Po = outside pressure of the bubble
r = radius of drop or bubble. - As drop is spherical, Pi > Po
∴ excess pressure inside drop = Pi − Po - Let the radius of drop increase from r to r + ∆r so that inside pressure remains constant.
- Initial area of drop A1 = 4πr2 ,
Final surface area of drop A2 = 4π (r + ∆r)2
Increase in surface area,
∆A = A2 − A1 = 4π[(r + ∆r)2 − r2]
= 4π[r2 + 2r∆r + ∆r2 − r2]
= 8πr∆r + 4π∆r2 - As ∆r is very small, the term containing ∆r2 can be neglected.
∴ dA = 8πr∆r - Work is done by a force of surface tension,
dW = TdA = (8πr∆r)T ….(1)
This work done is also equal to the product of the force F which causes an increase in the area of the bubble and the displacement Δr which is the increase in the radius of the bubble.
∴ dW = FΔr
The excess force is given by,
(Excess pressure) × (Surface area)
∴ F = (Pi – Po) × 4πr2
∴ dF = (Pi – Po)A
dW = F∆r = (Pi − Po) A∆r
From equation (1),
(Pi − Po) A∆r = (8πr∆r) T
∴ Pi − Po = `(8pirDeltarT)/(4pir^2Deltar)` ........(∵ A = 4πr2)
∴ Pi − Po = `(2T)/r` ….(2)
Equation (2) represents Laplace’s law of spherical membrane.
APPEARS IN
RELATED QUESTIONS
Draw a neat labelled diagram showing forces acting on the meniscus of water in a capillary tube.
Define the angle of contact.
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Explain why Water with detergent dissolved in it should have small angles of contact.
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
Define surface tension and surface energy.
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of soap solution is 30 dyne/cm. (Π = 3.142).
If a mosquito is dipped into water and released, it is not able to fly till it is dry again. Explain
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
By a surface of a liquid we mean
When water droplets merge to form a bigger drop
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
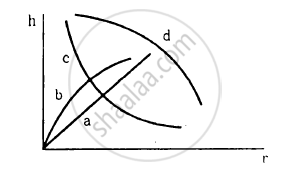
The properties of a surface are different from those of the bulk liquid because the surface molecules
(a) are smaller than other molecules
(b) acquire charge due to collision from air molecules
(c) find different type of molecules in their range of influence
(d) feel a net force in one direction.
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
The contact angle between a solid and a liquid is a property of
(a) the material of the solid
(b) the material of the liquid
(c) the shape of the solid
(d) the mass of the solid
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
The lower end of a capillary tube of radius 1 mm is dipped vertically into mercury. (a) Find the depression of mercury column in the capillary. (b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertical. Surface tension of mercury = 0.465 N m−1 and the contact angle of mercury with glass −135 °.
Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water = 0.075 Nm−1.
Consider an ice cube of edge 1.0 cm kept in a gravity-free hall. Find the surface area of the water when the ice melts. Neglect the difference in densities of ice and water.
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension the the thread. Surface tension of soap solution = 0.030 N m−1.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
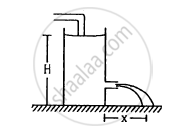
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Insect moves over the surface of water because of ______.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
The wear and tear in the machine part is due to ______.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
A soap bubble of radius 3 cm is formed inside another soap bubble of radius 6 cm. The radius of an equivalent soap bubble which has the same excess pressure as inside the smaller bubble with respect to the atmospheric pressure is ______ cm.
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
A liquid flows out drop by drop from a vessel through a vertical tube with an internal diameter of 2 mm, then the total number of drops that flows out during 10 grams of the liquid flow out ______. [Assume that the diameter of the neck of a drop at the moment it breaks away is equal to the internal diameter of tube and surface tension is 0.02 N/m].
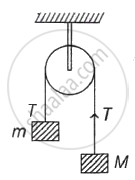
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Work done to blow a bubble of volume V is W. The work done in blowing a bubble of volume 2V will be ______.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
