Advertisements
Advertisements
Question
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
Solution
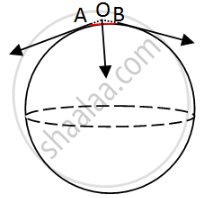
The forces act tangentially to the bubble surface on both sides of a given line but they have one component normal to the bubble surface. This component balances the force due to excess pressure inside the bubble.
In the figure, let us consider a small length AB on the surface of the spherical bubble. Let the surface forces act tangentially along A and B. On producing the forces backwards, they meet at a point O. By the parallelogram law of forces, we see that the resultant force acts opposite to the normal. This balances the internal forces due to excess pressure.
APPEARS IN
RELATED QUESTIONS
Derive an expression for excess pressure inside a drop of liquid.
Explain why Surface tension of a liquid is independent of the area of the surface
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of soap solution is 30 dyne/cm. (Π = 3.142).
If a mosquito is dipped into water and released, it is not able to fly till it is dry again. Explain
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
Viscosity is a property of
A 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water = 0.076 N m−1.
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
Consider an ice cube of edge 1.0 cm kept in a gravity-free hall. Find the surface area of the water when the ice melts. Neglect the difference in densities of ice and water.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
Water rises to a height of 20 mm in a capillary tube. If the radius made 1/3rd of its previous value, to what height will the water now rise in the tube?
Two soap bubbles have a radius in the ratio of 2:3. Compare the works done in blowing these bubbles.
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
The wettability of a surface by a liquid depends primarily on
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
The surface tension of a soap solution is T. The work done in blowing a soap bubble of diameter d to that of a diameter 2d is ______.
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
