Advertisements
Advertisements
Question
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
Solution 1
Given :
▪ Radius of capillary tube = 0.1 mm
▪ Surface tension of water = 7×10-2 N/m
▪ Angle of contact = 0°
▪ Density of water = 1000 kg/m
▪ Acceleration due to gravity = 9.8 m/s
To find:
▪ Height of water column inside the capillary tube.
Formula:
When a capillary tube of radius 'r' is dipped in a liquid of density ρ and surface tension T, the liquid rises or falls through a distance,
H = `(2"T" "cos" theta)/(rho "gr")`
H = `(2 xx 7 xx 10^-2 xx "cos" theta)/(1000 xx 9.8 xx 0.1 xx 10^-3)`
H = 0.142 m
Solution 2
Given:
r = 0.1 mm = 10−4 m,
T = 7 × 10−2 N/m,
θ = 0°,
ρ = 1000 kg/m3, g = 9.8 m/s2
To find: Height of capillary rise (h)
Formula: h = `(2Tcosθ)/(rρg)`
Calculation: From formula,
h = `(2 xx (7 xx 10^-2) xx cos0^circ)/(10^-4 xx 10^3 xx 9.8)`
= `(14 xx 10^-1)/(9.8)`
= `1/7`
= 0.1429 m
The rise of water inside the glass capillary is 0.1429 m.
RELATED QUESTIONS
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Angle of contact for the pair of pure water with clean glass is _______.
Define the angle of contact.
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Explain why Surface tension of a liquid is independent of the area of the surface
Define surface tension and surface energy.
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?
When water droplets merge to form a bigger drop
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
Viscosity is a property of
The properties of a surface are different from those of the bulk liquid because the surface molecules
(a) are smaller than other molecules
(b) acquire charge due to collision from air molecules
(c) find different type of molecules in their range of influence
(d) feel a net force in one direction.
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
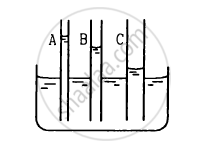
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water = 0.075 N m−1.
Consider an ice cube of edge 1.0 cm kept in a gravity-free hall. Find the surface area of the water when the ice melts. Neglect the difference in densities of ice and water.
Find the force exerted by the water on a 2 m2 plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface?
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Insect moves over the surface of water because of ______.
The water droplets are spherical in free fall due to ______
Define surface tension
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
How does the friction arise between the surfaces of two bodies in relative motion?
Describe an experiment to prove that friction depends on the nature of a surface.
The wettability of a surface by a liquid depends primarily on
Mention the S.I unit and dimension of surface tension.
How is surface tension related to surface energy?
Define the angle of contact for a given pair of solid and liquid.
What are the factors affecting the surface tension of a liquid?
Obtain an expression for the surface tension of a liquid by the capillary rise method.
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
The surface tension of the two liquids is respectively 20 and 60 dyne cm-1. The liquids drop from the ends of two tubes of the same radius. The ratio of the weights of the two drops is ______
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
A molecule of water on the surface experiences a net ______.
What is surface tension? Explain the applications of surface tension.
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
The free surface of oil in a tanker, at rest, is horizontal. If the tanker starts accelerating the free surface will be titled by an angle θ. If the acceleration is a ms–2, what will be the slope of the free surface?
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
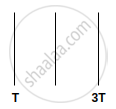
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
A liquid flows out drop by drop from a vessel through a vertical tube with an internal diameter of 2 mm, then the total number of drops that flows out during 10 grams of the liquid flow out ______. [Assume that the diameter of the neck of a drop at the moment it breaks away is equal to the internal diameter of tube and surface tension is 0.02 N/m].
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be ______.
