Advertisements
Advertisements
Question
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
Options
10 cm
\[10\sqrt{2}\] cm
\[10/\sqrt{2}\] cm
none of these
Solution
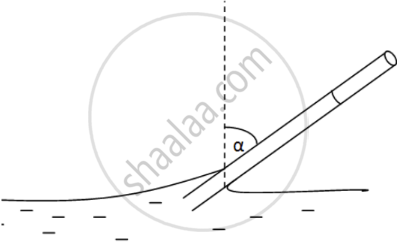
\[\text{ Given }: \]
\[\text{ l = 10 cm }\]
\[\alpha = {45}^0 \]
\[\text{ Rise in water level after the tube is tilted = h}\]
\[ \Rightarrow \text{ l = h} \cos {45}^0 \]
\[ \Rightarrow h = \frac{l}{\cos {45}^0} = \frac{10}{\left( \frac{1}{\sqrt{2}} \right)} = 10\sqrt{2}\text{ cm }\]
APPEARS IN
RELATED QUESTIONS
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
Explain why Surface tension of a liquid is independent of the area of the surface
Explain why Water with detergent dissolved in it should have small angles of contact.
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
A 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water = 0.076 N m−1.
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water = 0.075 N m−1.
Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water = 0.075 Nm−1.
A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. Water can be the minimum edge of the block so that it does not sink in water? Specific gravity of ice = 0.9.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

What will be the shape of the liquid meniscus for the obtuse angle of contact?
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
What is surface tension? Explain the applications of surface tension.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
A liquid flows out drop by drop from a vessel through a vertical tube with an internal diameter of 2 mm, then the total number of drops that flows out during 10 grams of the liquid flow out ______. [Assume that the diameter of the neck of a drop at the moment it breaks away is equal to the internal diameter of tube and surface tension is 0.02 N/m].
In a U-tube, the radii of two columns are respectively r1 and r2. When a liquid of density ρ(θ = 0°) is filled in it, a level difference of h is observed on two arms, then the surface tension of the liquid is ______.
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
