Advertisements
Advertisements
Question
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
Options
1:1
1:2
π:2
2:π
Solution
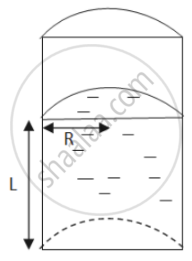
Let the height of the liquid-filled column be L.
Let the radius be denoted by R.
\[\text{ Total perimeter of the curved part = semi - circumference of upper area }= \pi r \]
\[\text{ Total surface tension force } = \pi RS\]
\[\text{ Total perimeter of the flat part = 2R } \]
\[\text{ Total surface tension force = 2RS }\]
\[\text{ Ratio of curved surface force to flat surface force } = \frac{\pi RS}{2RS} = \frac{\pi}{2}\]
\[\]
APPEARS IN
RELATED QUESTIONS
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Define surface tension and surface energy.
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
An ice cube is suspended in vacuum in a gravity free hall. As the ice melts it
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
Viscosity is a property of
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
A metal piece of mass 160 g lies in equilibrium inside a glass of water. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg/m3, find the normal force exerted by the bottom of the glass on the metal piece.

A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. Water can be the minimum edge of the block so that it does not sink in water? Specific gravity of ice = 0.9.
Explain the phenomena of surface tension on the basis of molecular theory.
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K–1, 1 atm. = 1.013 × 105 Pa; the membrane tension is 5 Nm–1.)
In a U-tube, the radii of two columns are respectively r1 and r2. When a liquid of density ρ(θ = 0°) is filled in it, a level difference of h is observed on two arms, then the surface tension of the liquid is ______.
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
