Advertisements
Advertisements
प्रश्न
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
पर्याय
1:1
1:2
π:2
2:π
उत्तर
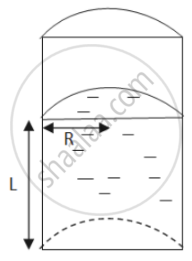
Let the height of the liquid-filled column be L.
Let the radius be denoted by R.
\[\text{ Total perimeter of the curved part = semi - circumference of upper area }= \pi r \]
\[\text{ Total surface tension force } = \pi RS\]
\[\text{ Total perimeter of the flat part = 2R } \]
\[\text{ Total surface tension force = 2RS }\]
\[\text{ Ratio of curved surface force to flat surface force } = \frac{\pi RS}{2RS} = \frac{\pi}{2}\]
\[\]
APPEARS IN
संबंधित प्रश्न
Explain why A drop of liquid under no external forces is always spherical in shape
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
If more air is pushed in a soap bubble, the pressure in it
If two soap bubbles of different radii are connected by a tube,
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.075 J m−2.
Define surface tension
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Obtain an expression for the capillary rise or fall using the forces method.
How does the friction arise between the surfaces of two bodies in relative motion?
What is capillarity?
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
Water rises in a capillary tube of radius r upto a height h. The mass of water in a capillary is m. The mass of water that will rise in a capillary of radius `"r"/4` will be ______.
A square frame of each side L is dipped in a soap solution and taken out. The force acting on the film formed is _____.
(T = surface tension of soap solution).
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
The excess of pressure, due to surface tension, on a spherical liquid drop of radius 'R' is proportional to ______.
The wear and tear in the machine part is due to ______.
The surface tension of a soap solution is T. The work done in blowing a soap bubble of diameter d to that of a diameter 2d is ______.
Work done to blow a bubble of volume V is W. The work done in blowing a bubble of volume 2V will be ______.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
