Advertisements
Advertisements
प्रश्न
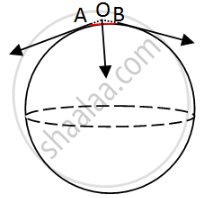
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
उत्तर
The forces act tangentially to the bubble surface on both sides of a given line but they have one component normal to the bubble surface. This component balances the force due to excess pressure inside the bubble.
In the figure, let us consider a small length AB on the surface of the spherical bubble. Let the surface forces act tangentially along A and B. On producing the forces backwards, they meet at a point O. By the parallelogram law of forces, we see that the resultant force acts opposite to the normal. This balances the internal forces due to excess pressure.
APPEARS IN
संबंधित प्रश्न
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
Define the angle of contact.
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
The total free surface energy of a liquid drop is `pisqrt2` times the surface tension of the liquid. Calculate the diameter of the drop in S.l. unit.
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
By a surface of a liquid we mean
If more air is pushed in a soap bubble, the pressure in it
If two soap bubbles of different radii are connected by a tube,
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
Define surface tension
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
The excess of pressure, due to surface tension, on a spherical liquid drop of radius 'R' is proportional to ______.
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
A water drop of radius R' splits into 'n' smaller drops, each of radius 'r'. The work done in the process is ______.
T = surface tension of water
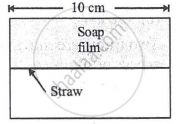
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
