Advertisements
Advertisements
प्रश्न
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
उत्तर
Given:
Radius of capillary tube r = 1 mm = 10−3 m
(a) Let T be the surface tension and ρ be the density of the liquid.
Then, for cos θ = 1, height (h) of liquid level:\[h = \frac{2T}{r\rho g}\] ........... (i),
where g is the acceleration due to gravity
\[\Rightarrow \text{ h } = \frac{2 \times \left( 0 . 076 \right)}{{10}^{- 3} \times 10 \times 100}\]
\[ = 1 . 52 \text{ cm} \]
\[ = 1 . 52 \times {10}^{- 2} \text{ m }\]
\[ = 1 . 52 \text{ cm }\]
(b) Let the new length of the tube be h'.
\[\text{ h }' = \frac{2T\cos \theta}{\text{ r }\rho \text{ g }}\]
\[\cos \theta = \frac{\text{ h'r }\rho g}{2T}\]
\[\text{ Using equation }\left( \text{ i } \right), \text{ we get: }\]
\[\cos \theta = \frac{h'}{h} = \frac{1}{2} \left( \text{ Because h' }= \frac{h}{2} \right)\]
\[ \Rightarrow \theta = \cos^{- 1} \left( \frac{1}{2} \right) = 60^\circ\]
The water surface in the capillary makes an angle of 60∘with the wall.
APPEARS IN
संबंधित प्रश्न
Explain why Surface tension of a liquid is independent of the area of the surface
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
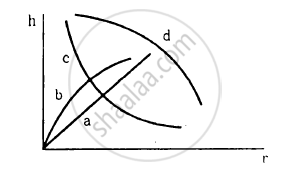
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
The properties of a surface are different from those of the bulk liquid because the surface molecules
(a) are smaller than other molecules
(b) acquire charge due to collision from air molecules
(c) find different type of molecules in their range of influence
(d) feel a net force in one direction.
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension the the thread. Surface tension of soap solution = 0.030 N m−1.
Find the force exerted by the water on a 2 m2 plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface?
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

Explain the phenomena of surface tension on the basis of molecular theory.
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
How does surface tension help a plant?
What is capillarity?
The surface tension of the two liquids is respectively 20 and 60 dyne cm-1. The liquids drop from the ends of two tubes of the same radius. The ratio of the weights of the two drops is ______
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
Under isothermal conditions, two soap bubbles of radii 'r1' and 'r2' coalesce to form a big drop. The radius of the big drop is ______.
The free surface of oil in a tanker, at rest, is horizontal. If the tanker starts accelerating the free surface will be titled by an angle θ. If the acceleration is a ms–2, what will be the slope of the free surface?
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
The surface tension of boiling water is ______.
