Advertisements
Advertisements
प्रश्न
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
पर्याय
4
2
1
0.125
उत्तर
Let the excess pressure inside the second bubble be P.
∴ Excess pressure inside the first bubble = 2P
Let the radius of the second bubble be R.
Let the radius of the first bubble be x.
\[\text{ Excess pressure inside the 2 nd soap bubble :} \]
\[P = \frac{4S}{R} . . . (1)\]
\[\text{ Excess pressure inside the 1st soap bubble: }\]
\[2P = \frac{4S}{x}\]
\[\text{ From (1), we get :} \]
\[2\left( \frac{4S}{R} \right) = \frac{4S}{x}\]
\[ \Rightarrow x = \frac{R}{2}\]
\[\text{ Volume of the first bubble }= \frac{4}{3} \pi x^3 \]
\[\text{ Volume of the second bubble } = \frac{4}{3} \pi R^3 \]
\[ \Rightarrow \frac{4}{3} \pi x^3 = n\frac{4}{3} \pi R^3 \]
\[ \Rightarrow x^3 = {nR}^3 \]
\[ \Rightarrow \left( \frac{R}{2} \right)^3 = {nR}^3 \]
\[ \Rightarrow n = \frac{1}{8} = 0 . 125\]
APPEARS IN
संबंधित प्रश्न
Explain why Surface tension of a liquid is independent of the area of the surface
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
Frictional force between solids operates even when they do not move with respect to each other. Do we have viscous force acting between two layers even if there is no relative motion?
If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?
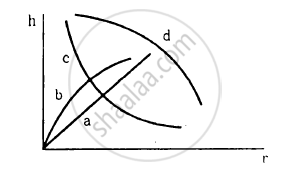
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
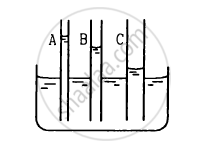
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

How much amount of work is done in forming a soap bubble of radius r?
Define surface tension
What are the factors affecting the surface tension of a liquid?
What is capillarity?
Why coffee runs up into a sugar lump (a small cube of sugar) when one corner of the sugar lump is held in the liquid?
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
The surface tension of a soap solution is T. The work done in blowing a soap bubble of diameter d to that of a diameter 2d is ______.
Define angle of contact.
