Advertisements
Advertisements
प्रश्न
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
उत्तर
Yes, the normal to the free surface of the liquid passes through the centre of the Earth. Because of the gravitational force, the free surface of the liquid takes the shape of the surface of the Earth. Also, because the gravitational force is directed towards the centre of the Earth, the normal to the free surface also passes through the centre of the Earth (in all cases).
APPEARS IN
संबंधित प्रश्न
Fill in the blanks using the word(s) from the list appended with each statement
Surface tension of liquids generally . . . with temperatures (increases / decreases)
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
When a sparingly soluble substance like alcohol is dissolved in water, surface tension of water
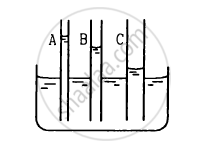
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water = 0.075 N m−1.
Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
A hollow spherical body of inner and outer radii 6 cm and 8 cm respectively floats half-submerged in water. Find the density of the material of the sphere.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Insect moves over the surface of water because of ______.
Explain the phenomena of surface tension on the basis of molecular theory.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be ______.
