Advertisements
Advertisements
प्रश्न
Explain the phenomena of surface tension on the basis of molecular theory.
उत्तर
Molecular theory of surface tension:
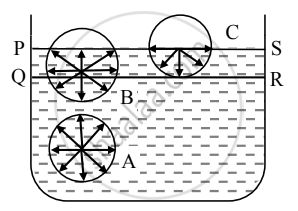
- Let PQRS = Surface film of liquid in a container containing liquid. PS is the free surface of the liquid and QR is the inner layer parallel to PS at distance equal to the range of molecular force.
- Now consider three molecules A, B, and C in a liquid in a vessel such that molecule A is well inside the liquid, molecule B within the surface film, and molecule C is on the surface of the liquid as shown in the figure.
- The sphere of influence of molecule A is entirely inside the liquid. As a result, molecule A is acted upon by equal cohesive forces in all directions. Thus, the net cohesive force acting on molecule A is zero.
- For molecule B, a large part of its sphere of influence is inside the liquid and a smaller part is outside the surface (in the air). The adhesive force acting on molecule B due to air molecules above it and within its sphere of influence is weak compared to the strong downward cohesive force acting on the molecule. As a result, molecule B gets attracted inside the liquid.
- For molecule C, half of the sphere of influence is in air and half is in liquid. As the density of air is much less than that of liquid, the number of air molecules within the sphere of influence of molecule C above the free surface of the liquid is much less than the numbers of liquid molecules within the sphere of influence that lies within the liquid. Thus, the adhesive force due to the air molecules acting on molecule C is weak compared to the cohesive force acting on the molecule. As a result, molecule C also gets attracted inside the liquid.
- Thus, all molecules in the surface film are acted upon by an unbalanced net cohesive force directed into the liquid. Therefore, the molecules in the surface film are pulled inside the liquid. This minimizes the total number of molecules in the surface film. As a result, the surface film remains under tension. The surface film of a liquid behaves like a stretched elastic membrane. This tension is known as surface tension and the force due to it acts tangential to the free surface of a liquid.
संबंधित प्रश्न
The energy of the free surface of a liquid drop is 5π times the surface tension of the liquid. Find the diameter of the drop in C.G.S. system.
The surface tension of water at 0°C is 75.5 dyne/cm. Calculate surface tension of water at 25°C.
(α for water = 2.7×10-3/°C)
Angle of contact for the pair of pure water with clean glass is _______.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
Explain why Surface tension of a liquid is independent of the area of the surface
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
Frictional force between solids operates even when they do not move with respect to each other. Do we have viscous force acting between two layers even if there is no relative motion?
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
If more air is pushed in a soap bubble, the pressure in it
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
The lower end of a capillary tube of radius 1 mm is dipped vertically into mercury. (a) Find the depression of mercury column in the capillary. (b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertical. Surface tension of mercury = 0.465 N m−1 and the contact angle of mercury with glass −135 °.
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
How much amount of work is done in forming a soap bubble of radius r?
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
The surface tension of a liquid at critical temperature is ______
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Water rises to a height of 20 mm in a capillary tube. If the radius made 1/3rd of its previous value, to what height will the water now rise in the tube?
Two soap bubbles have a radius in the ratio of 2:3. Compare the works done in blowing these bubbles.
Obtain an expression for the capillary rise or fall using the forces method.
How does surface tension help a plant?
Describe an experiment to prove that friction depends on the nature of a surface.
Explain elasticity using intermolecular forces.
How is surface tension related to surface energy?
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
Obtain an expression for the surface tension of a liquid by the capillary rise method.
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
What is surface tension? Explain the applications of surface tension.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
The angle of contact at the interface of water-glass is 0°, Ethylalcohol-glass is 0°, Mercury-glass is 140° and Methyliodide-glass is 30°. A glass capillary is put in a trough containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the trough is ______.
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
A soap bubble of radius 3 cm is formed inside another soap bubble of radius 6 cm. The radius of an equivalent soap bubble which has the same excess pressure as inside the smaller bubble with respect to the atmospheric pressure is ______ cm.
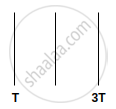
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
A liquid flows out drop by drop from a vessel through a vertical tube with an internal diameter of 2 mm, then the total number of drops that flows out during 10 grams of the liquid flow out ______. [Assume that the diameter of the neck of a drop at the moment it breaks away is equal to the internal diameter of tube and surface tension is 0.02 N/m].
The surface tension of a soap solution is T. The work done in blowing a soap bubble of diameter d to that of a diameter 2d is ______.
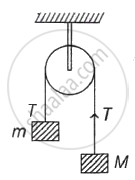
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
