Advertisements
Advertisements
प्रश्न
The energy of the free surface of a liquid drop is 5π times the surface tension of the liquid. Find the diameter of the drop in C.G.S. system.
उत्तर
Given that E = 5πT
Surface energy E = T dA -------- (Equation 1)
dA = 4πr2 -------- (where r is the radius of the liquid drop)
Substituting in Equation 1, we get
E = T * 4πr2
5πT = T* 4πr2 -------- (since E = 5πT)
`thereforer^2=5/4`
`thereforer=sqrt5/2`
Diameter, `d=2r=2*sqrt5/2`
`therefored=sqrt5=2.23cm`
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
The surface tension of water at 0°C is 75.5 dyne/cm. Calculate surface tension of water at 25°C.
(α for water = 2.7×10-3/°C)
Derive an expression for excess pressure inside a drop of liquid.
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Explain why Surface tension of a liquid is independent of the area of the surface
Explain why Water with detergent dissolved in it should have small angles of contact.
Explain why A drop of liquid under no external forces is always spherical in shape
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
A uniform vertical tube of circular cross section contains a liquid. The contact angle is 90°. Consider a diameter of the tube lying in the surface of the liquid. The surface to the right of this diameter pulls the surface on the left of it. What keeps the surface on the left in equilibrium?
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
An ice cube is suspended in vacuum in a gravity free hall. As the ice melts it
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
The contact angle between a solid and a liquid is a property of
(a) the material of the solid
(b) the material of the liquid
(c) the shape of the solid
(d) the mass of the solid
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J m−2.
The lower end of a capillary tube of radius 1 mm is dipped vertically into mercury. (a) Find the depression of mercury column in the capillary. (b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertical. Surface tension of mercury = 0.465 N m−1 and the contact angle of mercury with glass −135 °.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
Explain the capillary action.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Insect moves over the surface of water because of ______.
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
Mention the S.I unit and dimension of surface tension.
How is surface tension related to surface energy?
Distinguish between cohesive and adhesive forces.
What do you mean by capillarity or capillary action?
Obtain an expression for the surface tension of a liquid by the capillary rise method.
Water rises in a capillary tube of radius r upto a height h. The mass of water in a capillary is m. The mass of water that will rise in a capillary of radius `"r"/4` will be ______.
The surface tension of the two liquids is respectively 20 and 60 dyne cm-1. The liquids drop from the ends of two tubes of the same radius. The ratio of the weights of the two drops is ______
The excess of pressure, due to surface tension, on a spherical liquid drop of radius 'R' is proportional to ______.
A molecule of water on the surface experiences a net ______.
Why is raindrop spherical in nature?
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
A liquid flows out drop by drop from a vessel through a vertical tube with an internal diameter of 2 mm, then the total number of drops that flows out during 10 grams of the liquid flow out ______. [Assume that the diameter of the neck of a drop at the moment it breaks away is equal to the internal diameter of tube and surface tension is 0.02 N/m].
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
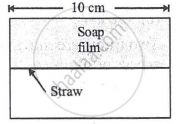
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
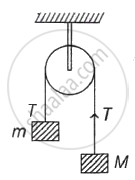
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Work done to blow a bubble of volume V is W. The work done in blowing a bubble of volume 2V will be ______.
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
