Advertisements
Advertisements
प्रश्न
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
पर्याय
when the mass is at the highest point
when the mass is at the lowest point
when the wire is horizontal
at an angle of cos−1(1/3) from the upward vertical.
उत्तर
If the velocity of the mass is a maximum at the bottom, then the string experiences tension due to both the weight of the mass and the high centrifugal force. Both these factors weigh the mass downwards. The tension is therefore, maximum at the lowest point, causing the string to most likely break at the bottom.
APPEARS IN
संबंधित प्रश्न
Define the angle of contact.
The surface tension of water at 0ºc is 75·5 dyne/cm. Find surface tension of water at 25°C. [ α for water = 0·0021/°C ]
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
Define surface tension and surface energy.
A uniform vertical tube of circular cross section contains a liquid. The contact angle is 90°. Consider a diameter of the tube lying in the surface of the liquid. The surface to the right of this diameter pulls the surface on the left of it. What keeps the surface on the left in equilibrium?
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
When the size of a soap bubble is increased by pushing more air in it, the surface area increases. Does it mean that the average separation between the surface molecules is increased?
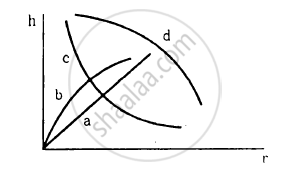
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
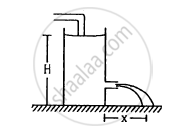
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Explain elasticity using intermolecular forces.
Water rises in a capillary tube of radius r upto a height h. The mass of water in a capillary is m. The mass of water that will rise in a capillary of radius `"r"/4` will be ______.
A square frame of each side L is dipped in a soap solution and taken out. The force acting on the film formed is _____.
(T = surface tension of soap solution).
Soap solution is used for cleaning dirty clothes because ______.
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be ______.
