Advertisements
Advertisements
प्रश्न
Derive an expression for capillary rise for a liquid having a concave meniscus.
उत्तर

The pressure due to the liquid (water) column of height h must be equal to the pressure difference 2T/R due to the concavity.
`therefore hrhog=(2T)/R`
where, ρ is the density of the liquid and g is acceleration due to gravity.
Let r be the radius of the capillary tube and θ be the angle of contact of the liquid as shown in the figure.
Then radius of curvature R of the meniscus is given by,
`R=r/costheta`
`therefore hrhog=(2Tcostheta)/r`
`therefore h=(2Tcostheta)/(rrhog)`
The above equation gives the expression for capillary rise (or fall) for a liquid. Narrower the tube, the greater is the height to which the liquid rises (or falls).
APPEARS IN
संबंधित प्रश्न
Derive an expression for excess pressure inside a drop of liquid.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
The surface tension of water at 0ºc is 75·5 dyne/cm. Find surface tension of water at 25°C. [ α for water = 0·0021/°C ]
Explain why Water with detergent dissolved in it should have small angles of contact.
Fill in the blanks using the word(s) from the list appended with each statement
Surface tension of liquids generally . . . with temperatures (increases / decreases)
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
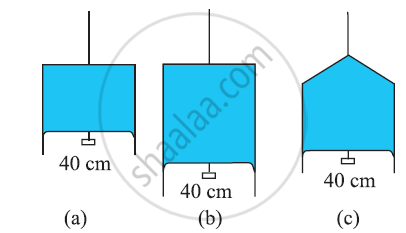
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
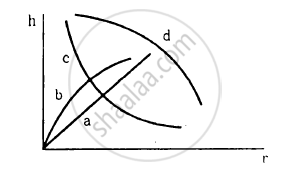
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
Find the excess pressure inside (a) a drop of mercury of radius 2 mm (b) a soap bubble of radius 4 mm and (c) an air bubble of radius 4 mm formed inside a tank of water. Surface tension of mercury, soap solution and water are 0.465 N m−1, 0.03 N m−1 and 0.076 N m−1 respectively.
The lower end of a capillary tube of radius 1 mm is dipped vertically into mercury. (a) Find the depression of mercury column in the capillary. (b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertical. Surface tension of mercury = 0.465 N m−1 and the contact angle of mercury with glass −135 °.
A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
A hollow spherical body of inner and outer radii 6 cm and 8 cm respectively floats half-submerged in water. Find the density of the material of the sphere.
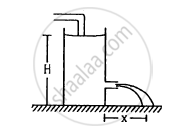
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
How much amount of work is done in forming a soap bubble of radius r?
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Insect moves over the surface of water because of ______.
Obtain an expression for the capillary rise or fall using the forces method.
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
The wettability of a surface by a liquid depends primarily on
Define the surface tension of a liquid.
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
A molecule of water on the surface experiences a net ______.
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
Soap solution is used for cleaning dirty clothes because ______.
What is surface tension? Explain the applications of surface tension.
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K–1, 1 atm. = 1.013 × 105 Pa; the membrane tension is 5 Nm–1.)
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
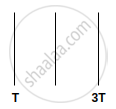
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
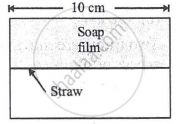
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
The surface tension of a soap solution is T. The work done in blowing a soap bubble of diameter d to that of a diameter 2d is ______.
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
