Advertisements
Advertisements
प्रश्न
Derive an expression for capillary rise for a liquid having a concave meniscus.
उत्तर

The pressure due to the liquid (water) column of height h must be equal to the pressure difference 2T/R due to the concavity.
`therefore hrhog=(2T)/R`
where, ρ is the density of the liquid and g is acceleration due to gravity.
Let r be the radius of the capillary tube and θ be the angle of contact of the liquid as shown in the figure.
Then radius of curvature R of the meniscus is given by,
`R=r/costheta`
`therefore hrhog=(2Tcostheta)/r`
`therefore h=(2Tcostheta)/(rrhog)`
The above equation gives the expression for capillary rise (or fall) for a liquid. Narrower the tube, the greater is the height to which the liquid rises (or falls).
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
The surface tension of water at 0°C is 75.5 dyne/cm. Calculate surface tension of water at 25°C.
(α for water = 2.7×10-3/°C)
Draw a neat labelled diagram showing forces acting on the meniscus of water in a capillary tube.
Define the angle of contact.
The surface tension of water at 0ºc is 75·5 dyne/cm. Find surface tension of water at 25°C. [ α for water = 0·0021/°C ]
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
The total energy of free surface of a liquid drop is 2π times the surface tension of the liquid. What is the diameter of the drop? (Assume all terms in SI unit).
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
State any two characteristics of the angle of contact
When a sparingly soluble substance like alcohol is dissolved in water, surface tension of water
The contact angle between water and glass is 0°. When water is poured in a glass to the maximum of its capacity, the water surface is convex upward. The angle of contact in such a situation is more than 90°. Explain.
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
By a surface of a liquid we mean
The properties of a surface are different from those of the bulk liquid because the surface molecules
(a) are smaller than other molecules
(b) acquire charge due to collision from air molecules
(c) find different type of molecules in their range of influence
(d) feel a net force in one direction.
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
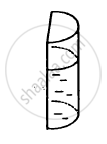
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
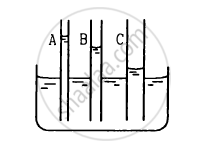
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly ______.
Explain the capillary action.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Define surface tension
A u-tube is made up of capillaries of bore 1 mm and 2 mm respectively. The tube is held vertically and partially filled with a liquid of surface tension 49 dyne/cm and zero angles of contact. Calculate the density of the liquid, if the difference in the levels of the meniscus is 1.25 cm. take g = 980 cm/s2
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
The wettability of a surface by a liquid depends primarily on
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
Obtain an expression for the surface tension of a liquid by the capillary rise method.
Why coffee runs up into a sugar lump (a small cube of sugar) when one corner of the sugar lump is held in the liquid?
The surface tension of the two liquids is respectively 20 and 60 dyne cm-1. The liquids drop from the ends of two tubes of the same radius. The ratio of the weights of the two drops is ______
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
A water drop of radius R' splits into 'n' smaller drops, each of radius 'r'. The work done in the process is ______.
T = surface tension of water
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
The wear and tear in the machine part is due to ______.
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
A coaxial cylinder made of glass is immersed in liquid of surface tension ' S'. Radius of inner and outer surface of cylinder are R1 and R2 respectively. Height till which liquid will rise is (Density of liquid is p):
When one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of capillary is ______.
(Surface tension of water = 7 × 10-2 N/m)
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
Define angle of contact.
