Advertisements
Advertisements
प्रश्न
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
Advertisements
उत्तर
i. Excess of pressure inside air bubble in a liquid: Consider an air bubble of radius R inside a liquid having surface tension T. Let P1 and P2 be the pressures outside and inside the air bubble, respectively.
Now, the excess pressure inside the air bubble is ∆P = P1 – P2
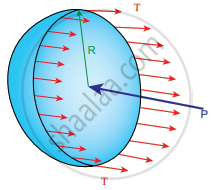
Air bubble
In order to find the excess pressure inside the air bubble, let us consider the forces acting on the air bubble. For the hemispherical portion of the bubble, considering the forces acting on it, we get,
- The force due to surface tension acting towards right around the rim of length 2πR is FT = 2πRT
- The force due to outside pressure P, is to the right acting across a cross-sectional area of πR2 is `"P"_1π"R"^2`
- The force due to pressure P2 inside the bubble, acting to the left is `"F"_("P"_2) = "P"_2π"R"^2`
As the air bubble is in equilibrium under the action of these forces, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
Excess pressure is ∆P = P2 – P1 = `(2"T")/"R"`
ii. Excess pressure inside a soap bubble: Consider a soap bubble of radius R and the surface tension of the soap bubble be T. A soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble. Therefore, the force on the soap bubble due to surface tension is 2 × 2πRT.
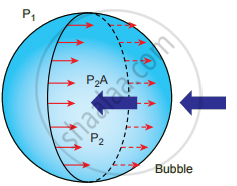
Soap bubble
The various forces acting on the soap bubble are,
- Force due to surface tension FT = 4πRT towards right.
- Force due to outside pressure, `"F"_("P"_1) = "P"_1π"R"^2` towards right
- Force due to inside pressure, `"F"_("P"_2) = "P"_2π"R"^2` towards left
As the bubble is in equilibrium, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
P2πR2 = 4πRT + P1πR2 ⇒ (P2 − P1)πR2 = 4πPT
Excess pressure is ∆P = P2 – P1 = `(4"T")/"R"`
iii. Excess pressure inside the liquid drop: Consider a liquid drop of radius R and the surface tension of the liquid is T.
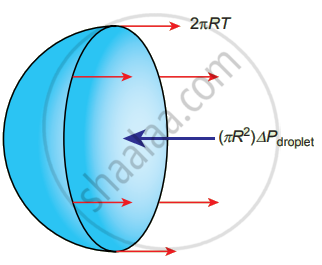
Liquid drop
The various forces acting on the liquid drop are,
- Force due to surface tension FT = 2πRT towards right
- Force due to outside pressure, `"F"_("P"_1) = "P"_1π"R"^2` towards right
- Force due to inside pressure, `"F"_("P"_2) = "P"_2π"R"^2` towards left
As the drop is in equilibrium, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
P2πR2 = 2πRT + P1πR2 ⇒ (P2 − P1)πR2 = 2πPT
Excess pressure is ∆P = P2 – P1 = `(2"T")/"R"`
APPEARS IN
संबंधित प्रश्न
The energy of the free surface of a liquid drop is 5π times the surface tension of the liquid. Find the diameter of the drop in C.G.S. system.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
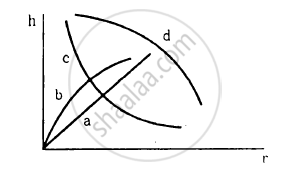
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly ______.
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
A square frame of each side L is dipped in a soap solution and taken out. The force acting on the film formed is _____.
(T = surface tension of soap solution).
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
