Advertisements
Advertisements
Question
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
Solution
i. Excess of pressure inside air bubble in a liquid: Consider an air bubble of radius R inside a liquid having surface tension T. Let P1 and P2 be the pressures outside and inside the air bubble, respectively.
Now, the excess pressure inside the air bubble is ∆P = P1 – P2
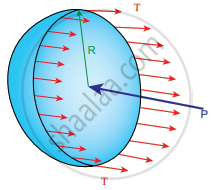
Air bubble
In order to find the excess pressure inside the air bubble, let us consider the forces acting on the air bubble. For the hemispherical portion of the bubble, considering the forces acting on it, we get,
- The force due to surface tension acting towards right around the rim of length 2πR is FT = 2πRT
- The force due to outside pressure P, is to the right acting across a cross-sectional area of πR2 is `"P"_1π"R"^2`
- The force due to pressure P2 inside the bubble, acting to the left is `"F"_("P"_2) = "P"_2π"R"^2`
As the air bubble is in equilibrium under the action of these forces, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
Excess pressure is ∆P = P2 – P1 = `(2"T")/"R"`
ii. Excess pressure inside a soap bubble: Consider a soap bubble of radius R and the surface tension of the soap bubble be T. A soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble. Therefore, the force on the soap bubble due to surface tension is 2 × 2πRT.
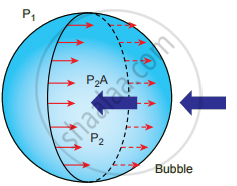
Soap bubble
The various forces acting on the soap bubble are,
- Force due to surface tension FT = 4πRT towards right.
- Force due to outside pressure, `"F"_("P"_1) = "P"_1π"R"^2` towards right
- Force due to inside pressure, `"F"_("P"_2) = "P"_2π"R"^2` towards left
As the bubble is in equilibrium, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
P2πR2 = 4πRT + P1πR2 ⇒ (P2 − P1)πR2 = 4πPT
Excess pressure is ∆P = P2 – P1 = `(4"T")/"R"`
iii. Excess pressure inside the liquid drop: Consider a liquid drop of radius R and the surface tension of the liquid is T.
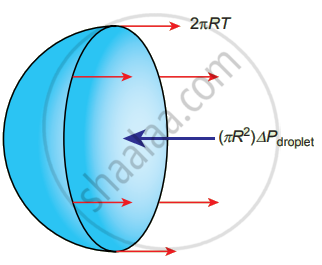
Liquid drop
The various forces acting on the liquid drop are,
- Force due to surface tension FT = 2πRT towards right
- Force due to outside pressure, `"F"_("P"_1) = "P"_1π"R"^2` towards right
- Force due to inside pressure, `"F"_("P"_2) = "P"_2π"R"^2` towards left
As the drop is in equilibrium, `"F"_("P"_2) = "F"_"T" + "F"_("P"_1)`
P2πR2 = 2πRT + P1πR2 ⇒ (P2 − P1)πR2 = 2πPT
Excess pressure is ∆P = P2 – P1 = `(2"T")/"R"`
APPEARS IN
RELATED QUESTIONS
Explain why A drop of liquid under no external forces is always spherical in shape
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
Obtain an expression for the surface tension of a liquid by the capillary rise method.
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
