Advertisements
Advertisements
प्रश्न
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

उत्तर
Given:
Specific gravity of water, \[\rho_W\] = 1 gm/cc
Specific gravity of ice, ρice = 0.9 gm/cc
Specific gravity of kerosene oil, ρk = 0.8 gm/cc
Now,
Vice = Vk + Vw
Here,
Vk = Volume of ice inside kerosene oil
Vw = Volume of ice inside water
Vice = Volume of ice
Thus, we have:
\[V_{ice} \times \rho_{ice} \times g = V_k \times \rho_k \times g + V_w \times \rho_w \times g\]
\[ \Rightarrow \left( V_k + V_w \right) \times \rho_{ice} = V_k \times \rho_k + V_w \times \rho_w \]
\[ \Rightarrow (0 . 9) V_k + (0 . 9) V_w = (0 . 8) V_k + \left( 1 \right) \times V_w \]
\[ \Rightarrow (0 . 1) V_w = 0 . 1 V_k \]
\[ \Rightarrow \frac{V_w}{V_k} = 1 . \]
\[ \Rightarrow V_w : V_k = 1: 1\]
APPEARS IN
संबंधित प्रश्न
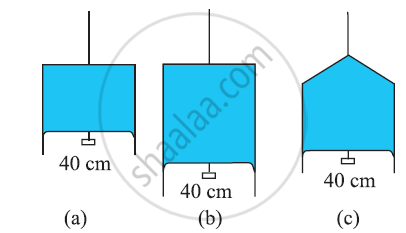
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?
When water droplets merge to form a bigger drop
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
The contact angle between a solid and a liquid is a property of
(a) the material of the solid
(b) the material of the liquid
(c) the shape of the solid
(d) the mass of the solid
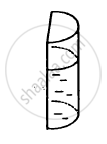
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water = 0.075 N m−1.
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Distinguish between cohesive and adhesive forces.
Obtain an expression for the surface tension of a liquid by the capillary rise method.
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
