Advertisements
Advertisements
प्रश्न
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
उत्तर
When a big drop of radius R, breaks into N droplets each of radius r, the volume remains constant.
∴ Volume of big drop = N × Volume of each small drop
`4/3 πR^3 = N xx 4/3 πR^3`
or `R^3 = Nr^3`
or `N = R^3/r^3`
Now, the change in surface area = `4πR^2 - N4πr^2`
= `4π(R^2 - Nr^2)`
The energy released = T × ΔA
= `S xx 4π(R^2 - Nr^2)` .....[T = Surface tension]
Due to releasing of this energy. the temperature is lowered.
If ρ is the density and s is the specific heat of liquid and its temperature is lowered by Δθ then the energy released = msΔθ ......[s = specific heat Δθ = change in temperature]
`T xx 4π(R^2 - Nr^2) = (4/3 xx R^3 xx ρ)sΔθ` ......`[∴m = vρ = 4/3 πR^3ρ]`
⇒ Δθ = `(T xx 4π(R^2 - Nr^2))/(4/3 πR^3 ρ xx s)`
= `(3T)/(ρs) [R^2/R^3 - (Nr^2)/R^3]`
= `(3T)/(ρs) [1/R - ((R^3-r^3) xx r^2)/R^3]`
= `(3T)/(ρs) [1/R - 1/r]`
APPEARS IN
संबंधित प्रश्न
Derive an expression for excess pressure inside a drop of liquid.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
Frictional force between solids operates even when they do not move with respect to each other. Do we have viscous force acting between two layers even if there is no relative motion?
Define the surface tension of a liquid.
Obtain an expression for the surface tension of a liquid by the capillary rise method.
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
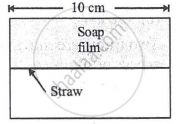
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.