Advertisements
Advertisements
प्रश्न
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
उत्तर १
Given:
r = 0.1 mm = 0.1 × 10−3 m,
T = 0.072 N/m
To find:
The change in surface energy.
Solution:
Let R be the radius of the single drop formed due to the coalescence of 27 droplets of mercury. Volume of 27 droplets = volume of the single drop as the volume of the liquid remains constant.
∴ `27 xx 4/3pi"r"^3 = 4/3pi"R"^3`
∴ `27"r"^3 = "R"^3`
∴ 3r = R
Surface area of 27 droplets = 27 × 4πr2 Surface area of single drop = 4πR2
∴ Decrease in surface area = `27 xx 4pi"r"^2 - 4pi"R"^2`
= `4pi (27"r"^2 - "R"^2)`
= `4pi[27"r"^2 - ("3r")^2]`
= `4pi xx 18"r"^2`
∴ The energy released = surface tension × decrease in surface area
= T × 4π × 18r2
= 0.072 × 4 × 3.142 × 18 × (1 × 10−4)2
= 1.628 × 10−7 J.
उत्तर २
Given:
r = 0.1 mm = 10−4 m,
n = 27,
T = 0.072 N/m
To find:
Change in surface energy (W)
Formula:
W = TdA
Calculation:
Volume of a single drop = `4/3piR^3` and
The volume of a single droplet = `4/3pir^3`
∴ We have, `4/3piR^3 = n xx 4/3pir^3` or R3 = nr3
∴ R = `root3 n r = root3 27 xx 10^-4 = 3 xx 10^-4`m2
From formula,
W = T (n × 4πr2 − 4πR2)
= 4πT(nr2 - R2)
= 4 × 3.142 × 0.072 × [27 × (10−4)2 − (3 × 10−4)2]
= 3.142 × 0.288 × 18 × 10−8
= 1.629 × 10−7 J
The change in the surface energy is 1.629 × 10−7 J.
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
The surface tension of water at 0°C is 75.5 dyne/cm. Calculate surface tension of water at 25°C.
(α for water = 2.7×10-3/°C)
Derive an expression for excess pressure inside a drop of liquid.
Angle of contact for the pair of pure water with clean glass is _______.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
Explain why Surface tension of a liquid is independent of the area of the surface
Explain why A drop of liquid under no external forces is always spherical in shape
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
Define surface tension and surface energy.
The total free surface energy of a liquid drop is `pisqrt2` times the surface tension of the liquid. Calculate the diameter of the drop in S.l. unit.
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of soap solution is 30 dyne/cm. (Π = 3.142).
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
If a mosquito is dipped into water and released, it is not able to fly till it is dry again. Explain
By a surface of a liquid we mean
When water droplets merge to form a bigger drop
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
The contact angle between a solid and a liquid is a property of
(a) the material of the solid
(b) the material of the liquid
(c) the shape of the solid
(d) the mass of the solid
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.075 J m−2.
Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water = 0.075 Nm−1.
A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
How much amount of work is done in forming a soap bubble of radius r?
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Explain the phenomena of surface tension on the basis of molecular theory.
Obtain an expression for the capillary rise or fall using the forces method.
How does surface tension help a plant?
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
The wettability of a surface by a liquid depends primarily on
Explain elasticity using intermolecular forces.
Define the surface tension of a liquid.
Obtain an expression for the surface tension of a liquid by the capillary rise method.
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
Why coffee runs up into a sugar lump (a small cube of sugar) when one corner of the sugar lump is held in the liquid?
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
Under isothermal conditions, two soap bubbles of radii 'r1' and 'r2' coalesce to form a big drop. The radius of the big drop is ______.
The wear and tear in the machine part is due to ______.
Why is raindrop spherical in nature?
The free surface of oil in a tanker, at rest, is horizontal. If the tanker starts accelerating the free surface will be titled by an angle θ. If the acceleration is a ms–2, what will be the slope of the free surface?
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
A soap bubble of radius 3 cm is formed inside another soap bubble of radius 6 cm. The radius of an equivalent soap bubble which has the same excess pressure as inside the smaller bubble with respect to the atmospheric pressure is ______ cm.
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
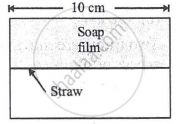
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
When one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of capillary is ______.
(Surface tension of water = 7 × 10-2 N/m)
Work done to blow a bubble of volume V is W. The work done in blowing a bubble of volume 2V will be ______.
