Advertisements
Advertisements
प्रश्न
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
उत्तर
Given:
Surface area of mercury drop, A = 1 mm2 = 10−6 m2
Radius of mercury drop, r = 4 mm = 4 × 10−3 m
Atmospheric pressure, P0 = 1.0 × 105 Pa
Surface tension of mercury, T = 0.465 N/m
(a) Force exerted by air on the surface area:
F = P0A
⇒ F= 1.0 × 105 × 10−6 = 0.1 N
(b) Force exerted by mercury below the surface area :
\[\text{ Pressure P' = P}_0 + \frac{2T}{\text{r}}\]
\[F = P'A = \left( P_0 + \frac{2T}{r} \right)A\]
\[ = \left( 0 . 1 + \frac{2 \times 0 . 465}{4 \times {10}^{- 3}} \right) \times {10}^{- 6} \]
\[ = 0 . 1 + 0 . 00023 = 0 . 10023 \text{N}\]
(c) Force exerted by mercury surface in contact with it:
\[P = \frac{2T}{r}\]
\[F = PA = \frac{2T}{r}A\]
\[ = \frac{2 \times 0 . 465}{4 \times {10}^{- 3}} \times {10}^{- 6} = 0 . 00023 \text{ N}\]
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Explain why Water with detergent dissolved in it should have small angles of contact.
State any two characteristics of the angle of contact
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
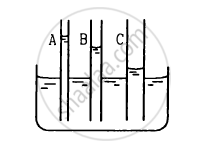
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. Water can be the minimum edge of the block so that it does not sink in water? Specific gravity of ice = 0.9.
Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
What will be the shape of the liquid meniscus for the obtuse angle of contact?
Mention the S.I unit and dimension of surface tension.
What are the factors affecting the surface tension of a liquid?
Obtain an expression for the excess of pressure inside a
- liquid drop
- liquid bubble
- air bubble
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
A water drop of radius R' splits into 'n' smaller drops, each of radius 'r'. The work done in the process is ______.
T = surface tension of water
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be ______.
