Advertisements
Advertisements
प्रश्न
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
Advertisements
उत्तर
Given:
Radius of the sphere, r = 5 cm
Mass of the maximum load, m = 0.1 kg
Let the weight of the sphere be W1 and the weight of the load be W2.
Now,
W1 + W2 = U
Here, U is the upward thrust.
Let V be the volume of the sphere.
\[\text{ Thus, we have: } \]
\[\text{mg + V }\times \rho_\text{s} \times \text{g = v } \times \rho_\text{w } \times \text{g}\]
\[\text{Here, }\]
\[ \rho_\text{ s }=\text{ Density of the sphere in gm/cc }\]
\[ \rho_\text{w }=\text{ Density of water }\]
\[\text{ On substituting the respective values in the above equation, we get: } \]
\[ (0 . 1) \times {10}^3 + \left( \frac{4}{3} \right) \times \pi \times (5 )^3 \times \rho_s = \left( \frac{4}{3} \right) \times \pi \times (5 )^3 \times 1\]
\[ \Rightarrow 100 = \left( \frac{4}{3} \right) \times \pi \times 125 \times (1 - \rho_\text{s} )\]
\[ \Rightarrow 1 - \rho_\text{s} = \frac{3 \times 100}{4 \times \pi \times 125} = 0 . 19\]
\[ \Rightarrow \rho_\text{s} = 1 - (0 . 19)\]
\[ = 0 . 81 \text{ gm/cc = 0 . 8 gm/cc}\]
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
Derive an expression for excess pressure inside a drop of liquid.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Explain why Water with detergent dissolved in it should have small angles of contact.
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
If more air is pushed in a soap bubble, the pressure in it
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.
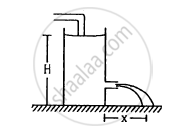
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
A molecule of water on the surface experiences a net ______.
Under isothermal conditions, two soap bubbles of radii 'r1' and 'r2' coalesce to form a big drop. The radius of the big drop is ______.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
The angle of contact at the interface of water-glass is 0°, Ethylalcohol-glass is 0°, Mercury-glass is 140° and Methyliodide-glass is 30°. A glass capillary is put in a trough containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the trough is ______.
The free surface of oil in a tanker, at rest, is horizontal. If the tanker starts accelerating the free surface will be titled by an angle θ. If the acceleration is a ms–2, what will be the slope of the free surface?
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
