Advertisements
Advertisements
प्रश्न
Explain the phenomena of surface tension on the basis of molecular theory.
उत्तर
Molecular theory of surface tension:
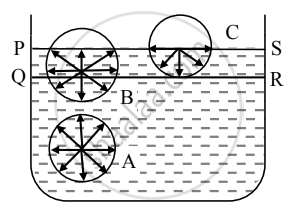
- Let PQRS = Surface film of liquid in a container containing liquid. PS is the free surface of the liquid and QR is the inner layer parallel to PS at distance equal to the range of molecular force.
- Now consider three molecules A, B, and C in a liquid in a vessel such that molecule A is well inside the liquid, molecule B within the surface film, and molecule C is on the surface of the liquid as shown in the figure.
- The sphere of influence of molecule A is entirely inside the liquid. As a result, molecule A is acted upon by equal cohesive forces in all directions. Thus, the net cohesive force acting on molecule A is zero.
- For molecule B, a large part of its sphere of influence is inside the liquid and a smaller part is outside the surface (in the air). The adhesive force acting on molecule B due to air molecules above it and within its sphere of influence is weak compared to the strong downward cohesive force acting on the molecule. As a result, molecule B gets attracted inside the liquid.
- For molecule C, half of the sphere of influence is in air and half is in liquid. As the density of air is much less than that of liquid, the number of air molecules within the sphere of influence of molecule C above the free surface of the liquid is much less than the numbers of liquid molecules within the sphere of influence that lies within the liquid. Thus, the adhesive force due to the air molecules acting on molecule C is weak compared to the cohesive force acting on the molecule. As a result, molecule C also gets attracted inside the liquid.
- Thus, all molecules in the surface film are acted upon by an unbalanced net cohesive force directed into the liquid. Therefore, the molecules in the surface film are pulled inside the liquid. This minimizes the total number of molecules in the surface film. As a result, the surface film remains under tension. The surface film of a liquid behaves like a stretched elastic membrane. This tension is known as surface tension and the force due to it acts tangential to the free surface of a liquid.
संबंधित प्रश्न
'n' droplets of equal size of radius r coalesce to form a bigger drop of radius R. The energy liberated is equal to...................
(T =Surface tension of water)
`(a) 4piR^2T[n^(1/3)-1]`
`(b) 4pir^2T[n^(1/3)-1]`
`(c) 4piR^2T[n^(2/3)-1]`
`(d)4 pir^2T[n^(2/3)-1]`
The surface tension of water at 0ºc is 75·5 dyne/cm. Find surface tension of water at 25°C. [ α for water = 0·0021/°C ]
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Explain why Surface tension of a liquid is independent of the area of the surface
Explain why A drop of liquid under no external forces is always spherical in shape
Fill in the blanks using the word(s) from the list appended with each statement
Surface tension of liquids generally . . . with temperatures (increases / decreases)
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of soap solution is 30 dyne/cm. (Π = 3.142).
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
Air is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution in S, the work done in the process is
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
A 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water = 0.076 N m−1.
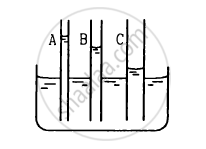
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.075 J m−2.
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
Consider an ice cube of edge 1.0 cm kept in a gravity-free hall. Find the surface area of the water when the ice melts. Neglect the difference in densities of ice and water.
A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
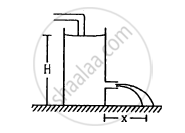
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, the density of water = 1000 kg/m3, g = 9.8 m/s2.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyn/cm.
Water rises to a height of 20 mm in a capillary tube. If the radius made 1/3rd of its previous value, to what height will the water now rise in the tube?
Describe an experiment to prove that friction depends on the nature of a surface.
Explain elasticity using intermolecular forces.
How is surface tension related to surface energy?
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
A water drop of radius R' splits into 'n' smaller drops, each of radius 'r'. The work done in the process is ______.
T = surface tension of water
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
Soap solution is used for cleaning dirty clothes because ______.
The wear and tear in the machine part is due to ______.
What is surface tension? Explain the applications of surface tension.
The angle of contact at the interface of water-glass is 0°, Ethylalcohol-glass is 0°, Mercury-glass is 140° and Methyliodide-glass is 30°. A glass capillary is put in a trough containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the trough is ______.
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K–1, 1 atm. = 1.013 × 105 Pa; the membrane tension is 5 Nm–1.)
A coaxial cylinder made of glass is immersed in liquid of surface tension ' S'. Radius of inner and outer surface of cylinder are R1 and R2 respectively. Height till which liquid will rise is (Density of liquid is p):
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
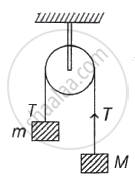
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
The surface tension of soap solution is 25 × 10-3 Nm-1. The excess of pressure inside a soap bubble of diameter 1 cm is ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
