Advertisements
Advertisements
प्रश्न
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
उत्तर
Diameter of the first bore, d1 = 3.0 mm = 3 × 10–3 m
Hence the radius of the first bore, `r_1 = d_1/2 = 1.5 xx 10^(-3) m`
Diameter of the second bore, `d_2`= 6.0 mm
Hence the radius of the second bore, `r_2 = d_2/2 = 3xx 10^(-3) m`
Surface tension of water `s = 7.3 xx 10^(-2) Nm^(-1)`
Angle of contact between the bore surface and water, θ= 0
Density of water, ρ =1.0 × 103 kg/m–3
Acceleration due to gravity, g = 9.8 m/s2
Let h1 and h2 be the heights to which water rises in the first and second tubes respectively. These heights are given by the relations:
`h_1 = (2s cos theta)/(r_1rhog)` ...(i)
`h_2 = (2scos theta)/(r_2rhog)` ...(ii)
The difference between the levels of water in the two limbs of the tube can be calculated as:
`= (2 s cos theta)/(r_1rhog) - (2 s cos theta)/(r_2rhog)`
`= (2 s cos theta)/(rhog)[1/r_1 - 1/r_2]`
`= (2xx 7.3 xx 10^(-2) xx 1)/(1xx10^3xx9.8) [1/(1.5xx10^(-3)) - 1/(3xx10^(-3))]`
`= 4.966 xx 10^(-3) m`
= 4.97 mm
Hence, the difference between levels of water in the two bores is 4.97 mm.
APPEARS IN
संबंधित प्रश्न
The energy of the free surface of a liquid drop is 5π times the surface tension of the liquid. Find the diameter of the drop in C.G.S. system.
State any two characteristics of the angle of contact
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
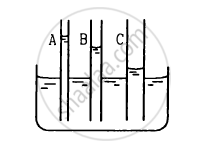
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J m−2.
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
Insect moves over the surface of water because of ______.
What are the factors affecting the surface tension of a liquid?
What is surface tension? Explain the applications of surface tension.
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
