Advertisements
Advertisements
प्रश्न
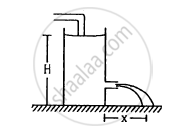
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
उत्तर
It is given that H is the height of the cylindrical vessel.
Now, let h be the height of the hole from the surface of the tank.
The velocity of water \[\left( v \right)\] is given by
\[v = \sqrt{2g(H - h)}\]
Also, let t be the time of flight.
Now,
\[t = \sqrt{\frac{2h}{g}}\]
Let x be the maximum horizontal distance .
\[ \therefore x = v \times t\]
\[ = \sqrt{2g(H - h)} \times \sqrt{\frac{2h}{g}}\]
\[ = \sqrt{4(Hh - h^2 )}\]
For x to be maximum,
\[\frac{d}{dh}\left( Hh - h^2 \right) = 0\]
\[ \Rightarrow 0 = H - 2h\]
\[ \Rightarrow h = \frac{H}{2}\]
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
When a glass capillary tube is dipped at one end in water, water rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy?
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
Viscosity is a property of
Find the excess pressure inside (a) a drop of mercury of radius 2 mm (b) a soap bubble of radius 4 mm and (c) an air bubble of radius 4 mm formed inside a tank of water. Surface tension of mercury, soap solution and water are 0.465 N m−1, 0.03 N m−1 and 0.076 N m−1 respectively.
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water = 0.075 N m−1.
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J m−2.
Find the force exerted by the water on a 2 m2 plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface?
How does the friction arise between the surfaces of two bodies in relative motion?
How does surface tension help a plant?
Obtain an expression for the surface tension of a liquid by the capillary rise method.
The surface tension of the two liquids is respectively 20 and 60 dyne cm-1. The liquids drop from the ends of two tubes of the same radius. The ratio of the weights of the two drops is ______
Soap solution is used for cleaning dirty clothes because ______.
The wear and tear in the machine part is due to ______.
What is surface tension? Explain the applications of surface tension.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
